Understanding Bayes' Theorem

A Comprehensive Exploration Using Venn Diagrams

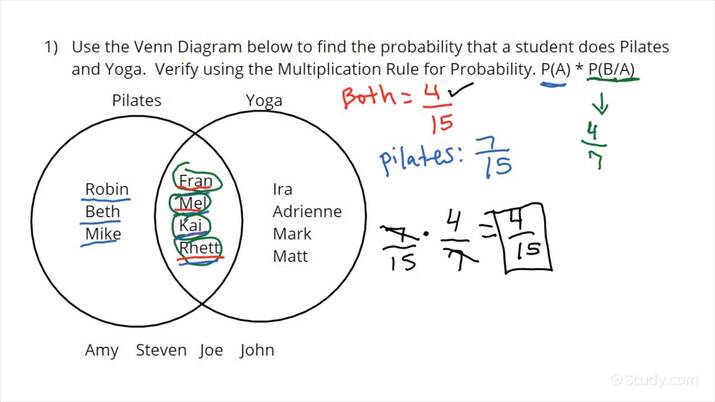
Highlights

Visualizing Events: Venn diagrams allow for clear visualization of events and their intersections.
Conditional Probabilities: The overlapping sections represent conditional probabilities like P(A|B) and P(B|A).
Intuitive Updates: Bayes' theorem explains how new evidence updates our prior beliefs into posterior probabilities.

Introduction to Bayes' Theorem

Bayes' theorem is a cornerstone of probability theory and statistics, offering a method to update the probability estimates of an event in the light of new data or evidence. It allows us to revisit our initial assumptions (known as 'priors') and adjust them when taking new evidence into account, resulting in revised estimates (known as 'posteriors'). More specifically, the theorem relates various forms of conditional probability and helps us understand how evidence modifies our prediction of an event.

Fundamental Concepts and Notations

To build a robust understanding of Bayes' theorem, it's essential to first grasp several fundamental terms:

Events and Sample Space

In probability theory, an event is a set comprising outcomes from the sample space, which is the collection of all possible outcomes. In our context, an event might be the occurrence of a disease, the test result being positive, or any other phenomenon we wish to analyze.

Conditional Probability

Conditional probability, denoted as \( \text{\( P(A|B) \)} \), is the likelihood of event A occurring given that event B has already occurred. Conceptually, this means restricting our analysis only to the subset of outcomes in which event B happens and computing the probability that event A also occurs.

The conditional probability is mathematically defined as:

\( \displaystyle P(A|B) = \frac{P(A \cap B)}{P(B)} \)

Bayes' Theorem Formula

Bayes' theorem itself is written as:

\( \displaystyle P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \)

Here:

\( \displaystyle P(A|B) \) is the posterior probability – the probability of event A after taking into account event B.
\( \displaystyle P(B|A) \) is the likelihood – how likely it is to observe event B given that A is true.
\( \displaystyle P(A) \) is the prior probability of event A before considering any evidence.
\( \displaystyle P(B) \) is the probability of event B occurring under all conditions.

Utilizing Venn Diagrams to Understand Bayes' Theorem

Venn diagrams serve as powerful tools for visually breaking down these probabilistic events. By representing events as circles within a rectangle (which symbolizes the complete sample space), we can more easily comprehend the relationships between different events and their interactions.

Step-by-Step Illustration with Venn Diagrams

1. The Universe and Events

Begin with a rectangle representing the entire sample space, or the universe (U), where every possible outcome exists. Within this rectangle, draw two overlapping circles—one representing event A and the other representing event B.

The entire area of circle A corresponds to the probability \( \displaystyle P(A) \), while the entire area of circle B corresponds to \( \displaystyle P(B) \). The overlapping section of these circles represents those scenarios where both events occur simultaneously, denoted as \( \displaystyle P(A \cap B) \).

2. Representing Conditional Probabilities

To visually interpret the conditional probability \( \displaystyle P(A|B) \), focus exclusively on circle B. The probability \( \displaystyle P(A|B) \) is then depicted as the fraction of circle B’s area that overlaps with circle A.

Likewise, should you wish to evaluate \( \displaystyle P(B|A) \), you would concentrate on circle A and assess what proportion of its area is shared with circle B.

3. Visualizing the Bayes' Theorem Equation

Recall that Bayes' theorem is given by:

\( \displaystyle P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \)

Inside the Venn diagram, the intersection \( \displaystyle P(A \cap B) \) can be viewed from two angles:

It is part of event B when calculating \( \displaystyle P(A|B) \), or
It is part of event A when examining \( \displaystyle P(B|A) \).

Thus, you can see that understanding the size and proportion of the overlap directly leads to insights about these conditional probabilities. The diagram makes it clear that once event B occurs, the “new sample space” consists solely of its area, and the overlapping region reveals how likely A is to occur in this restricted context.

Interpreting Bayes' Theorem Through a Practical Example

Let’s apply these concepts to a real-world scenario—the evaluation of medical test results.

Example: Medical Test for a Disease

Scenario Setup

Consider the following:

Event A: A patient has a specific disease.
Event B: A patient tests positive for that disease.

We are interested in determining \( \displaystyle P(A|B) \)—the probability that a patient actually has the disease given a positive test result. This calculation, however, isn’t as straightforward as reading off the test result. We need to take into account factors like the test’s accuracy (reflected in \( \displaystyle P(B|A) \)), the general prevalence of the disease (or \( \displaystyle P(A) \)), and the overall rate of positive test results (or \( \displaystyle P(B) \)).

Venn Diagram Representation

In the Venn diagram:

The entire rectangle represents all patients.
Circle A represents patients who actually have the disease.
Circle B embodies patients who test positive.
The overlapping region between circle A and circle B indicates those patients who both have the disease and test positive (true positives), corresponding to \( \displaystyle P(A \cap B) \).

By carefully analyzing these areas, we visually capture how likely it is that a patient who tests positive truly has the disease. The size of the overlap relative to the total area of circle B gives the conditional probability \( \displaystyle P(A|B) \). This is precisely what Bayes' theorem quantifies through its formula.

Numerical Illustration

Assume we define:

Parameter	Interpretation	Example Value
\( P(A) \)	Prior probability of having the disease	0.01 (or 1%)
\( P(B\|A) \)	Sensitivity or probability of testing positive if diseased	0.99 (or 99%)
\( P(B) \)	Overall probability of testing positive	0.05 (or 5%)

Using Bayes' theorem:

\( \displaystyle P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} = \frac{0.99 \times 0.01}{0.05} \)

This numerical example demonstrates how, even with a highly sensitive test, a low prevalence of the disease can lead to a relatively low probability \( \displaystyle P(A|B) \) that someone who tests positive actually has the condition. The Venn diagram visually reinforces this concept by showing that the overlap (true positives) might be small relative to the entire area that represents positive test results.

Benefits of the Venn Diagram Approach

Visual methods such as Venn diagrams provide several advantages when learning about Bayes' theorem:

Enhanced Intuition

By converting abstract probabilities into concrete areas, Venn diagrams help build an intuitive understanding of how probabilities relate and interact. They make it easier to see the impact of new evidence on existing beliefs.

Clear Visualization of Relationships

Drawing overlapping circles clarifies the relationship between the overall probability of an event, the probability of the intersection, and the conditional probabilities. Students and practitioners can visually gauge the influence and significance of the overlap.

Simplified Complex Calculations

When dealing with multiple events or scenarios, Venn diagrams help break down the problem into visually manageable components, reducing the cognitive load and facilitating error checking in probability calculations.

Advanced Considerations of Visual Representation

While the basic two-circle Venn diagram is sufficient for explaining simple cases of Bayes' theorem, more complex scenarios might involve multiple events. In such cases, additional circles or nested diagrams can be used to illustrate the conditional relationships among the different events. However, the principles remain fundamentally similar—each diagram still emphasizes the relationships between the likelihoods and prior probabilities.

It is important to note that while Venn diagrams are excellent for building intuition and presenting an overview of the relationships, they might not capture all nuances in cases involving continuous distributions or multiple conditional dependencies. For such complex models, additional mathematical tools and graphical representations (like probability trees or network diagrams) might be required.

Synthesized Visualization Table

Component	Description	Venn Diagram Representation
\( P(A) \)	Prior probability or overall probability of event A occurring	Area of Circle A relative to the sample space
\( P(B) \)	Overall probability of event B occurring	Area of Circle B relative to the sample space
\( P(A \cap B) \)	Joint probability where both events A and B occur	Overlap area between circles A and B
\( P(A\|B) \)	Conditional probability of A given B	Proportion of Circle B’s area that is also in Circle A
\( P(B\|A) \)	Conditional probability of B given A	Proportion of Circle A’s area that is also in Circle B