Logic

A Comprehensive Exploration of Reasoning and Argumentation

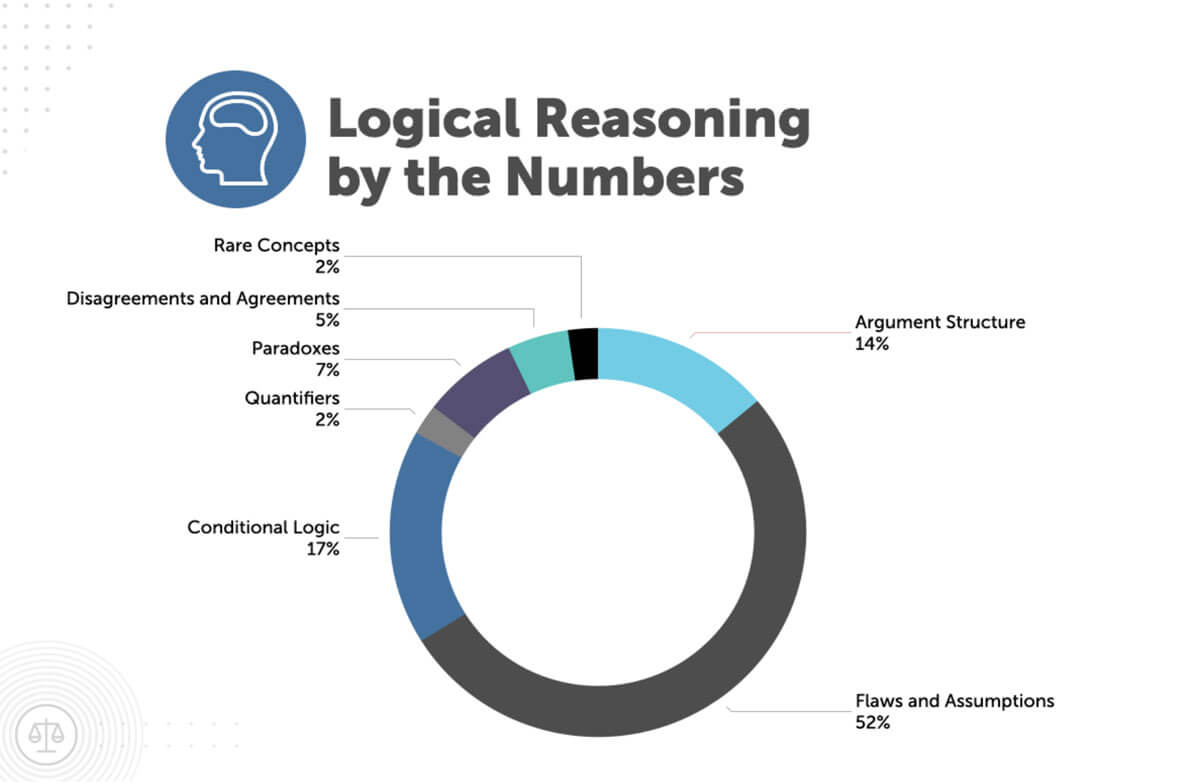
Key Takeaways

Logic provides the foundational framework for distinguishing valid from invalid reasoning.
It encompasses various branches, including formal and informal logic, each serving unique purposes and applications.
Mastering logic enhances critical thinking, problem-solving, and decision-making skills across diverse disciplines.

Introduction to Logic

What is Logic?

Logic is the systematic study of the principles that govern valid reasoning and argumentation. It seeks to establish the rules and structures that determine whether a line of reasoning is sound and whether conclusions logically follow from premises. Logic serves as a foundational element in various fields, including philosophy, mathematics, computer science, linguistics, and law, enabling individuals to analyze arguments, solve problems, and make informed decisions.

The Importance of Logic

Understanding logic is essential for developing strong analytical skills and fostering clear, coherent thinking. It equips individuals with the ability to evaluate the strengths and weaknesses of arguments, identify fallacies, and construct persuasive reasoning. In academic and professional settings, logic is indispensable for conducting research, devising strategies, programming computers, and formulating policies. Moreover, logic enhances everyday decision-making by promoting rational and objective analysis of information.

Branches of Logic

Formal Logic

Formal logic focuses on the abstract structures of arguments, utilizing symbolic representations to analyze the validity of inferences. It emphasizes the form over the content of statements, allowing for precise and unambiguous analysis. Formal logic is instrumental in mathematics and computer science, where exact reasoning is crucial.

Subfields of Formal Logic

Propositional Logic: Deals with statements that are either true or false and the logical relationships between them.
Predicate Logic: Extends propositional logic by incorporating quantifiers and predicates, enabling more detailed and expressive statements.
Modal Logic: Examines concepts of necessity and possibility, allowing for the analysis of statements that express different modes of truth.
Temporal Logic: Focuses on reasoning about sequences of events in time, useful in computer science for program verification.

Informal Logic

Informal logic pertains to the study of natural language arguments and everyday reasoning. Unlike formal logic, it emphasizes the content, context, and pragmatic aspects of arguments. Informal logic is valuable in areas such as law, rhetoric, and critical thinking, where arguments are often complex and context-dependent.

Key Components of Informal Logic

Argument Analysis: Evaluating the strength and validity of arguments presented in ordinary language.
Fallacy Identification: Recognizing common errors in reasoning that undermine the logic of arguments.
Argument Construction: Building coherent and persuasive arguments by organizing premises and conclusions effectively.

Symbolic and Mathematical Logic

This branch employs mathematical symbols and formal systems to represent logical expressions and relationships. Symbolic logic is foundational in computer science, especially in the development of programming languages, algorithms, and software engineering. It allows for the precise formulation and manipulation of logical statements, facilitating automated reasoning and verification processes.

Applications in Computer Science

Algorithm Design: Using logical principles to create efficient and effective algorithms for problem-solving.
Programming Languages: Developing languages that support logical operations and data structures for computational tasks.
Artificial Intelligence: Implementing logical frameworks for machine reasoning, decision-making, and learning.

Philosophical Logic

Philosophical logic explores the foundational and abstract aspects of reasoning, delving into areas such as semantics, epistemology, and metaphysics. It investigates the nature of logical truths, the relationship between language and thought, and the principles that underlie rational inquiry. Philosophical logic often intersects with other disciplines, contributing to a deeper understanding of knowledge, reality, and cognition.

Topics in Philosophical Logic

Semantics: Studying the meaning and interpretation of logical expressions and statements.
Epistemic Logic: Analyzing knowledge, belief, and information within logical frameworks.
Deontic Logic: Examining normative concepts such as obligation, permission, and prohibition.

Core Concepts of Logic

Arguments and Inferences

At the heart of logic lies the concept of the argument. An argument is a structured sequence of propositions where one or more premises are intended to support a conclusion. The strength and validity of an argument depend on the logical connections between premises and the conclusion.

Definitions

Premise: A statement or proposition that provides support or evidence for the conclusion.
Conclusion: The statement that the premises are intended to support or prove.
Inference: The logical process of deriving the conclusion from the premises.

Propositions

Propositions are declarative statements that express claims or assertions and possess a truth value, being either true or false. They are the fundamental building blocks of arguments, serving as premises or conclusions within logical structures.

Characteristics of Propositions

Clarity: Propositions must be clearly and unambiguously stated to be effectively analyzed.
Truth Value: Each proposition must be capable of being evaluated as true or false.
Independence: Individual propositions should stand independently to avoid confusion in logical analysis.

Validity and Soundness

An argument's validity and soundness are critical measures of its logical strength.

Validity

An argument is valid if the conclusion logically follows from the premises, regardless of the actual truth of the premises. In other words, if the premises are true, the conclusion must also be true.

Soundness

An argument is sound if it is both valid and its premises are indeed true. Soundness guarantees the truth of the conclusion.

Laws of Thought

Classical logic is founded on the fundamental laws of thought, which are essential for maintaining consistency in reasoning.

The Three Laws

Law of Identity: Asserts that an entity is identical to itself (A is A).
Law of Non-Contradiction: States that contradictory propositions cannot both be true simultaneously (A cannot be both A and not A).
Law of the Excluded Middle: Declares that for any proposition, either it is true or its negation is true, with no middle ground (A is either true or false).

Types of Reasoning

Deductive Reasoning

Deductive reasoning involves deriving specific conclusions from general premises with certainty. If the premises are true and the reasoning is valid, the conclusion must also be true. This form of reasoning is foundational in mathematics and formal logic.

Example of Deductive Reasoning

Consider the following argument:

Premise 1: All humans are mortal.
Premise 2: Socrates is a human.
Conclusion: Therefore, Socrates is mortal.

Here, the conclusion is necessarily true if both premises are true, exemplifying deductive certainty.

Inductive Reasoning

Inductive reasoning involves making generalizations based on specific observations or evidence. Unlike deduction, induction does not guarantee the truth of the conclusion but suggests its likelihood. This form of reasoning is prevalent in scientific inquiry and everyday decision-making.

Example of Inductive Reasoning

Consider the following argument:

Premise: The sun has risen in the east every morning recorded.
Conclusion: The sun will rise in the east tomorrow.

While the conclusion is probable based on past observations, it is not absolutely certain, demonstrating the probabilistic nature of inductive reasoning.

Abductive Reasoning

Abductive reasoning seeks the most plausible explanation for a set of observations or facts. It involves forming hypotheses that best explain the available evidence, often used in scientific research and diagnostic processes.

Example of Abductive Reasoning

Consider the following scenario:

Observation: The lawn is wet in the morning.
Possible Explanations: It rained overnight; the sprinkler system was activated; someone watered the lawn manually.
Conclusion: The most plausible explanation is that it rained overnight.

Abductive reasoning leads to a probable explanation based on the available evidence.

Applications of Logic

Philosophy and Ethics

In philosophy, logic is indispensable for constructing and deconstructing arguments, analyzing concepts, and exploring abstract theories. It aids in clarifying thoughts, resolving paradoxes, and enhancing the rigor of philosophical discourse. In ethics, logical reasoning helps evaluate moral arguments, establish ethical principles, and navigate complex moral dilemmas.

Mathematics

Mathematical logic underpins the foundations of mathematics, providing the structure for mathematical proofs, theorems, and problem-solving methodologies. It ensures the consistency and validity of mathematical systems, enabling the exploration of abstract concepts and the development of new mathematical theories.

Computer Science

Logic is fundamental to computer science, informing the design and implementation of algorithms, programming languages, and software systems. It facilitates automated reasoning, artificial intelligence, and the development of computational models. Logical principles enable the creation of efficient, reliable, and scalable technological solutions.

Law

Legal reasoning relies heavily on logic to construct coherent arguments, interpret statutes, and evaluate evidence. Lawyers and judges use logical analysis to assess the validity of claims, identify inconsistencies, and ensure that legal decisions are based on sound reasoning and factual accuracy.

Critical Thinking and Everyday Reasoning

In everyday life, logic enhances critical thinking and decision-making by providing tools to evaluate the validity of information, identify biases, and construct persuasive arguments. It assists individuals in navigating complex situations, solving problems, and making informed choices based on rational analysis.

Logical Fallacies

Logical fallacies are errors in reasoning that undermine the logic of arguments. They can occur unintentionally or be used deliberately to manipulate or deceive. Recognizing and avoiding fallacies is crucial for maintaining logical integrity and engaging in truthful, persuasive discourse.

Common Logical Fallacies

Ad Hominem

The ad hominem fallacy involves attacking the character or motives of the person making an argument rather than addressing the argument itself. This diversionary tactic seeks to undermine the opponent's credibility instead of engaging with their reasoning.

Straw Man

The straw man fallacy occurs when someone misrepresents an opponent's argument to make it easier to attack or refute. By exaggerating, distorting, or oversimplifying the original argument, the opponent's position becomes vulnerable to criticism.

False Dilemma

The false dilemma fallacy presents only two options or outcomes when, in fact, more exist. This oversimplification forces a choice between limited alternatives, disregarding the complexity and variety of possible solutions.

Circular Reasoning

Circular reasoning involves using the conclusion of an argument as one of its premises, creating a loop that offers no real proof or justification. This fallacy fails to provide independent support for the conclusion, rendering the argument logically ineffective.

Post Hoc Ergo Propter Hoc

This fallacy assumes that because one event followed another, the first event caused the second. It conflates correlation with causation without establishing a causal link between the events.

Hasty Generalization

Hasty generalization occurs when a conclusion is drawn based on insufficient or biased evidence. It involves making broad claims without adequate data to support them, leading to inaccurate or unreliable conclusions.

Red Herring

The red herring fallacy introduces irrelevant information or distractions to divert attention away from the main issue. This tactic obscures the argument's focus, preventing a logical evaluation of the original topic.

Historical Development of Logic

Ancient Foundations

The study of logic has ancient origins, with significant contributions from early Greek philosophers. Aristotle is renowned for developing syllogistic logic, a system that uses deductive reasoning to derive conclusions from premises. His work laid the groundwork for subsequent developments in logical theory.

Medieval and Enlightenment Advances

During the medieval period, scholars expanded upon Aristotle's foundations, integrating logic with theological and philosophical inquiries. The Enlightenment era saw further advancements, with thinkers like René Descartes and Immanuel Kant contributing to the refinement of logical principles and the exploration of new logical paradigms.

Modern Formal Logic

The late 19th and early 20th centuries marked the emergence of modern formal logic, driven by mathematicians and philosophers such as Gottlob Frege, Bertrand Russell, and Ludwig Wittgenstein. Innovations in symbolic notation and the development of formal systems revolutionized logical analysis, enabling more precise and versatile applications of logic in various disciplines.

Contemporary Developments

In contemporary times, logic continues to evolve, incorporating advancements from computer science, cognitive science, and linguistics. The development of non-classical logics, such as fuzzy logic and quantum logic, addresses the complexities of modern reasoning and expands the applicability of logical principles to diverse and emerging fields.

Principles and Laws of Logic

Law of Identity

The Law of Identity is one of the foundational principles of logic. It states that an entity is identical to itself; formally, A is A. This principle ensures consistency within logical systems by maintaining that each entity has a distinct and unchanging identity.

Law of Non-Contradiction

The Law of Non-Contradiction asserts that contradictory statements cannot both be true at the same time and in the same respect. Formally, it can be expressed as ¬(A ∧ ¬A), meaning that it is not the case that both A and not A are true simultaneously. This law prevents the coexistence of opposing claims, maintaining logical coherence.

Law of the Excluded Middle

The Law of the Excluded Middle posits that for any proposition, either it is true or its negation is true; there is no middle ground. Formally, this is represented as A ∨ ¬A. This principle ensures that every proposition has a definitive truth value, eliminating ambiguity and fostering clear-cut reasoning.

Practical Applications of Logic

Logic in Programming and Software Development

In programming, logic is integral to writing efficient and error-free code. Logical operators such as AND, OR, and NOT are fundamental in controlling the flow of programs, making decisions, and handling conditions. Logical reasoning is also essential in debugging, algorithm design, and optimizing software performance.

Logic in Artificial Intelligence

Artificial Intelligence (AI) relies heavily on logic for reasoning, learning, and decision-making. Logical frameworks enable AI systems to process information, infer conclusions, and adapt to new data. Logic-based AI applications include expert systems, natural language processing, and automated theorem proving.

Logic in Scientific Research

Scientific research utilizes logic to formulate hypotheses, design experiments, and interpret results. Logical analysis ensures that scientific theories are consistent, evidence-based, and capable of predicting phenomena. Logic also plays a role in statistical reasoning, enabling scientists to draw valid conclusions from data.

Logic in Everyday Life

In daily life, logic aids in making informed decisions, solving problems, and evaluating information. Whether planning activities, managing finances, or engaging in discussions, logical thinking helps individuals assess options, anticipate outcomes, and choose the most rational courses of action.

Enhancements: Logical Representations and Examples

Logical Representations

Logic employs various symbols and notations to represent propositions and their relationships. These representations facilitate precise communication and analysis of complex arguments.

Common Logical Symbols

∧ (AND): Represents logical conjunction, indicating that both propositions are true.
∨ (OR): Represents logical disjunction, indicating that at least one proposition is true.
¬ (NOT): Represents negation, indicating the opposite of a proposition's truth value.
→ (IMPLIES): Represents implication, indicating that if one proposition is true, another follows.
↔ (IF AND ONLY IF): Represents bi-conditional, indicating that two propositions are equivalent.

Example: Propositional Logic

Consider the following propositions:

P: It is raining.
Q: The ground is wet.

The implication P → Q states that if it is raining, then the ground is wet. This can be represented in symbolic form as:


% Representing the implication: If P then Q
p :- % It is raining
q :- % The ground is wet

% Defining the implication
p_implies_q :- p, p -> q, q.

In this example, the conclusion q (the ground is wet) logically follows from premise p (it is raining).

Example: Syllogistic Logic

Syllogistic logic involves deducing conclusions from two premises. For instance:

Premise 1: All humans are mortal.
Premise 2: Socrates is a human.
Conclusion: Therefore, Socrates is mortal.

This syllogism demonstrates deductive reasoning, where the conclusion is necessitated by the premises.

Advanced Topics in Logic

Non-Classical Logics

Non-classical logics deviate from classical logical principles to address specific limitations or to model different types of reasoning. They include:

Fuzzy Logic

Fuzzy logic allows for reasoning with degrees of truth rather than binary true/false values. It is useful in handling uncertainty and imprecision, such as in control systems and decision-making processes.

Modal Logic

Modal logic extends classical logic by introducing modalities like necessity and possibility. It is employed in various fields, including philosophy, computer science, and linguistics, to model scenarios involving possibility, necessity, and temporal aspects.

Temporal Logic

Temporal logic incorporates time into logical systems, enabling the representation and analysis of propositions that change over time. It is particularly useful in verifying the correctness of computer programs and digital circuits over time.

Quantum Logic

Quantum logic arises from the principles of quantum mechanics, where classical logical laws do not always apply. It addresses the unique behaviors of quantum systems, such as superposition and entanglement, enabling logical analysis within the quantum framework.

Paraconsistent Logic

Paraconsistent logic tolerates contradictions without collapsing into triviality. It allows for the coexistence of contradictory statements, making it valuable in fields where inconsistent information must be managed, such as legal reasoning and artificial intelligence.

Logical Reasoning in Practice

Constructing Valid Arguments

Building valid arguments involves ensuring that the conclusion logically follows from the premises. This requires careful structuring of premises, adherence to logical principles, and avoidance of fallacies. A valid argument maintains coherence and persuasiveness through rigorous logical connections.

Steps to Construct a Valid Argument

Identify the Conclusion: Clearly state the main point or assertion you intend to support.
Gather Supporting Premises: Collect relevant statements or evidence that bolster the conclusion.
Ensure Logical Consistency: Verify that the premises do not contradict each other and that they collectively support the conclusion.
Avoid Logical Fallacies: Be vigilant in preventing common reasoning errors that could undermine the argument's validity.
Review and Refine: Critically assess the argument to ensure clarity, coherence, and logical strength.

Evaluating Arguments

Assessing the strength of arguments involves evaluating both the logical structure and the truthfulness of the premises. A thorough evaluation examines whether the reasoning is sound, the premises are accurate, and the conclusion is justified.

Criteria for Evaluation

Validity: Does the conclusion logically follow from the premises?
Soundness: Are the premises true and reliable?
Relevance: Do the premises directly support the conclusion?
Avoidance of Fallacies: Is the argument free from common reasoning errors?
Clarity and Precision: Is the argument clearly articulated and unambiguous?

Logical Reasoning Techniques

Syllogisms

Syllogisms are structured arguments consisting of two premises and a conclusion. They serve as fundamental examples of deductive reasoning, demonstrating how conclusions can be derived logically from given premises.

Types of Syllogisms

Categorical Syllogism: Involves statements that assert or deny that all or some of the members of one category are included in another category.
Conditional Syllogism: Involves "if-then" statements, where the conclusion follows from the conditional relationship established in the premises.
Disjunctive Syllogism: Involves "either-or" statements, where the conclusion follows by eliminating one of the alternatives.

Venn Diagrams

Venn diagrams are graphical representations used to illustrate logical relationships between different sets or categories. They visually depict the overlap and distinctions between propositions, aiding in the analysis of syllogistic arguments and set theory concepts.

Using Venn Diagrams in Logic

Visualizing Relationships: Display how different sets interact, overlap, or remain distinct.
Evaluating Validity: Determine the logical consistency and validity of arguments by visual inspection.
Teaching Tool: Facilitate the understanding of complex logical concepts through visual aids.

Truth Tables

Truth tables are systematic tables used to explore the truth values of logical expressions based on their components. They provide a comprehensive overview of all possible scenarios, enabling the analysis of logical consistency and the identification of tautologies or contradictions.

Components of Truth Tables

Columns: Represent individual propositions and the logical operators connecting them.
Rows: Enumerate all possible truth value combinations for the propositions involved.
Outputs: Display the resulting truth value of the logical expression for each combination.

Logical Proofs

Logical proofs involve a series of deductive steps that establish the truth of a conclusion based on accepted premises and logical rules. Proofs demonstrate the validity of propositions and the logical connections between them, providing rigorous justification for theoretical claims.

Types of Proofs

Direct Proof: Proves a proposition by straightforward logical deduction from known premises.
Indirect Proof: Involves assuming the negation of the conclusion and deriving a contradiction to establish validity.
Proof by Contradiction: Similar to indirect proof, it involves demonstrating that the negation of the conclusion leads to an inconsistency.
Proof by Induction: Used primarily in mathematics, it establishes the truth of an infinite sequence of propositions by proving a base case and an inductive step.

Challenges and Limitations of Logic

Complexity of Natural Language

Natural language is inherently complex and nuanced, making it challenging to apply formal logical systems directly. Ambiguities, context-dependencies, and idiomatic expressions can complicate the translation of everyday language into formal logic, necessitating careful interpretation and analysis.

Handling Uncertainty and Vagueness

Traditional logic operates on binary truth values, which can be limiting when dealing with uncertainty, partial truths, or probabilistic scenarios. Extensions such as fuzzy logic and probabilistic logic address these limitations by allowing for degrees of truth and modeling uncertainty more effectively.

Gödel's Incompleteness Theorems

Kurt Gödel's incompleteness theorems revealed fundamental limitations within formal logical systems. The first theorem states that in any sufficiently powerful logical system, there exist true statements that cannot be proven within the system. The second theorem asserts that such a system cannot demonstrate its own consistency, highlighting inherent constraints in formal logical frameworks.

Paradoxes

Logical paradoxes present situations where seemingly valid reasoning leads to contradictory or absurd conclusions. Paradoxes challenge the consistency and completeness of logical systems, prompting revisions and the development of more robust logical frameworks to address such anomalies.

Logic in Modern Technology

Search Algorithms and Logic

Search algorithms utilize logical principles to navigate data structures, retrieve information, and optimize search results. Logical conditions and decision-making processes are integral to the efficiency and accuracy of search functionalities in databases, search engines, and information retrieval systems.

Logic Programming

Logic programming is a paradigm that uses formal logic to express computational logic. Languages like Prolog enable the representation of facts and rules, allowing for automated reasoning and problem-solving through query-based interactions. Logic programming is used in various applications, including artificial intelligence, natural language processing, and knowledge representation.

Automated Theorem Proving

Automated theorem proving involves the use of software to prove mathematical theorems automatically. Logical algorithms and formal proof systems enable computers to verify the validity of complex mathematical statements, advancing research in mathematics and computer science.

Enhancements: Logical Representations and Examples

Logical Expressions

Logical expressions are combinations of propositions connected by logical operators. They represent complex statements and are fundamental in constructing and analyzing arguments.

Example of a Logical Expression

Consider the following expression:

P: It is raining.
Q: The ground is wet.

The expression P ∧ Q represents the logical conjunction "It is raining and the ground is wet." The expression P → Q represents the implication "If it is raining, then the ground is wet."

Truth Tables

Truth tables enumerate all possible truth values of logical expressions, providing a clear and systematic way to evaluate their validity.

Sample Truth Table

P	Q	P ∧ Q	P ∨ Q	P → Q
True	True	True	True	True
True	False	False	True	False
False	True	False	True	True
False	False	False	False	True

Logical Proof Example

Below is an example of a direct proof using modus ponens, a fundamental rule of inference in formal logic.


% Defining propositions
p :- % It is raining
q :- % The ground is wet

% Modus Ponens: If P then Q, P is true, therefore Q is true
modus_ponens :- p, p -> q, q.

In this proof, given that P (it is raining) is true and P implies Q (if it is raining, then the ground is wet), we can conclude Q (the ground is wet) is true.

Conclusion

Logic stands as a pivotal discipline that underpins effective reasoning and argumentation across numerous fields. Its systematic approach to evaluating the validity of inferences ensures clarity, coherence, and reliability in thought processes. By encompassing diverse branches such as formal and informal logic, symbolic and mathematical logic, and philosophical logic, the study of logic offers comprehensive tools for analyzing complex arguments, solving intricate problems, and making informed decisions. Mastery of logical principles not only enhances academic and professional endeavors but also enriches everyday life by fostering critical thinking and rational analysis. As technology and knowledge continue to advance, the role of logic remains integral, driving innovation and enabling deeper understanding of the world and our interactions within it.

References

merriam-webster.com

Logic Definition & Meaning - Merriam-Webster

en.wikipedia.org

Logic - Wikipedia

britannica.com

Logic | Definition, Types & Uses - Britannica

philosophy.hku.hk

What is logic? - Philosophy@HKU