
Unraveling Numeric Enigmas: A Comprehensive Guide to Decrypting Number-Based Ciphers
Explore the fascinating world of cryptography by understanding and deciphering numerical codes.
Key Decryption Insights
- Context is Crucial: Without knowing the specific cipher used, decrypting number sequences is highly challenging. Various ciphers convert letters to numbers differently, making a universal decryption method impossible.
- Common Number-Based Ciphers: The most common and easily decipherable number-to-letter cipher is A1Z26, where A=1, B=2, and so on. Other ciphers like Base 26, ASCII, and even numeric keypad draws also exist.
- Tools and Techniques for Decryption: Online multi-decoders and cipher identifiers are invaluable resources. They leverage frequency analysis and extensive databases to suggest possible ciphers and aid in breaking codes.
The sequence of numbers you've provided—47 45 85 77 87 77 56 95 77 54 68 65, 86 66 58 87 22 96 46 66 89 45 97 75 55, and 46 24 77—presents an intriguing challenge in the realm of cryptography. Decrypting such a sequence requires understanding the underlying encryption method, often referred to as a cipher. Without explicit knowledge of the cipher or its key, the task becomes akin to solving a puzzle with missing pieces.
The Challenge of Ambiguity in Numeric Ciphers
Why knowing the cipher is paramount for successful decryption.
The primary hurdle in decrypting a numerical sequence without context is the sheer variety of ways letters and numbers can be interconverted. A number like "47" could represent anything depending on the cipher: it could be a single letter in an advanced cipher, part of a multi-digit number representing a letter, or even a coordinate in a more complex system like a book cipher. Many online tools for decryption emphasize that knowing the encryption used is the first and most crucial step. Without this, decryption is often impossible, especially for shorter messages where statistical analysis is less effective.
Exploring Potential Number-Based Ciphers
A look into common methods for converting letters to numbers.
When dealing with numbers that represent letters, several standard ciphers come to mind. Each operates on a different principle, leading to diverse numerical representations for the same plaintext.
The A1Z26 Cipher: A Simple Substitution
The A1Z26 cipher is perhaps the most straightforward number-to-letter conversion. In this method, each letter of the alphabet is assigned a numerical value corresponding to its position: A=1, B=2, C=3, and so on, up to Z=26. This cipher is commonly used for educational purposes and recreational puzzles due to its simplicity. For decryption, you merely replace each number with its corresponding letter. If the numbers in your sequence were intended for A1Z26, they would typically be between 1 and 26. The presence of numbers like "47," "85," or "97" in your sequence immediately suggests that A1Z26 is unlikely to be the sole or primary cipher, as these numbers exceed the standard 1-26 range. However, it's possible these numbers are part of a more complex structure, perhaps two-digit numbers that combine to form larger values or use a different numerical base.

An illustration representing the concept of letters and numbers in a jigsaw puzzle format, symbolizing their interchangeable nature in ciphers.
Beyond A1Z26: Other Numeric Transformations
Beyond the basic A1Z26, cryptography offers other methods to encode text into numbers:
- Base 26 Cipher: This cipher treats words as numbers in a base-26 system, where each position corresponds to a power of 26, similar to how decimal numbers use powers of 10. For instance, DCODE can be represented as \(3 \times 26^4 + 2 \times 26^3 + 14 \times 26^2 + 3 \times 26^1 + 4 \times 26^0\), where A=0, B=1, etc. This results in relatively large numbers for even short words.
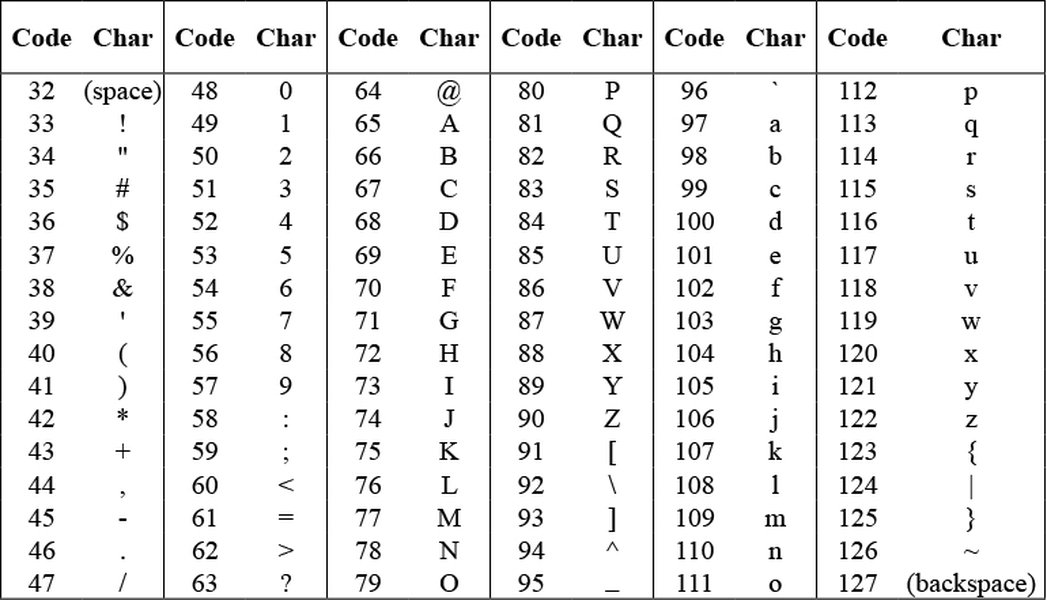
- ASCII Codes: Each character (letters, numbers, symbols) has a corresponding ASCII (American Standard Code for Information Interchange) value. For example, 'A' is 65, 'B' is 66, and so on. Many numbers in your sequence (e.g., 65, 66, 68, 75, 77, 85, 86, 87, 89, 95, 96, 97) fall within or near the ASCII range for uppercase letters (65-90) and some symbols or lowercase letters. This makes ASCII a strong candidate for parts of your sequence.
- Numeric Keypad Draw Cipher: This involves representing letters by the path drawn on a numeric keypad (e.g., 1-2-3 for A). This method generates sequences of digits that, when connected on a keypad, form a recognizable shape.
- Book Ciphers: In a book cipher, numbers refer to specific locations (page, line, word, or character number) within a known text. Decryption requires access to the exact book or text used as the key.
Decryption Strategy and Tools
Systematic approaches and online aids for code-breaking.
Given the complexity of the numbers provided, a multi-faceted approach is necessary. Generic decryption tools often employ frequency analysis and other statistical methods to identify patterns and suggest possible ciphers.
Leveraging Online Decoders and Cipher Identifiers
Online multi-decoders are designed to solve a wide range of codes and ciphers. These tools can analyze the input text, search for codewords, and attempt to decrypt messages based on known cipher types. They often look for common letter distributions, character repetitions, and word lengths to narrow down possibilities. If a message is too short, however, frequency analysis may not be effective. In such cases, knowing external clues, such as keywords, alphabets, or specific numerical bases, becomes paramount. Some sophisticated cipher identifiers even utilize artificial intelligence to recognize encryption types and link to relevant decryption tools.
Manual Analysis and Pattern Recognition
Even with advanced tools, a degree of manual analysis can be beneficial. Observing the ranges of numbers, their grouping, and any recurring patterns can provide hints. For instance, the consistent appearance of two-digit numbers might suggest a system where each number corresponds to a specific character or a pair of characters. The comma separators in your sequence could indicate divisions between words or distinct coded segments.
A Closer Look at the Provided Sequences with ASCII as a Hypothesis
Hypothesizing an ASCII interpretation for the numerical strings.
Let's consider the possibility that some of these numbers represent ASCII values. The ASCII range for uppercase letters is 65-90. Let's try to convert the numbers falling within this range:
| Original Number | ASCII Character (if applicable) | Observation/Context |
|---|---|---|
| 47 | / (Slash) | Could be a separator or a coded character. |
| 45 | - (Hyphen) | Commonly used as a separator or dash. |
| 85 | U | Falls within uppercase alphabet. |
| 77 | M | Falls within uppercase alphabet. |
| 87 | W | Falls within uppercase alphabet. |
| 77 | M | Falls within uppercase alphabet. |
| 56 | 8 | A numeral itself, potentially part of a larger number or direct digit. |
| 95 | _ (Underscore) | Could be a space or separator. |
| 77 | M | Falls within uppercase alphabet. |
| 54 | 6 | A numeral itself. |
| 68 | D | Falls within uppercase alphabet. |
| 65 | A | Falls within uppercase alphabet. |
| 86 | V | Falls within uppercase alphabet. |
| 66 | B | Falls within uppercase alphabet. |
| 58 | : (Colon) | Could be a separator. |
| 22 | (N/A) | Too low for standard ASCII letters (A=65), but could be A1Z26 if 22=V. |
| 96 | ` (Grave accent) | Could be a separator or a non-alphabetic character. |
| 46 | . (Period) | A common punctuation mark. |
| 89 | Y | Falls within uppercase alphabet. |
| 75 | K | Falls within uppercase alphabet. |
| 55 | 7 | A numeral itself. |
| 24 | (N/A) | Too low for standard ASCII letters, but could be A1Z26 if 24=X. |
Applying an ASCII interpretation to the provided sequence yields a mixed result with letters, numbers, and symbols. This suggests that if ASCII is involved, it might be combined with another cipher, or the numbers outside the typical letter range have a different encoding scheme. For instance, "22" and "24" are too low to be ASCII letters but could be A1Z26 values for 'V' and 'X' respectively, indicating a hybrid cipher.
Understanding Cipher Complexity and Decryptability
A radar chart illustrating the challenges of various ciphers.
To better understand the inherent difficulties in deciphering various codes, especially when no key is provided, we can consider a radar chart. This chart will visually represent the complexity, resistance to frequency analysis, and key dependency of several common cipher types, including those that deal with numbers.
This radar chart illustrates that simpler ciphers like A1Z26 and ASCII encoding are high on "Ease of Recognition" and low on "Key Dependency" and "Resistance to Frequency Analysis." However, when numbers fall outside expected ranges, or if the cipher is more complex (like Base 26 or Vigenere), "Ambiguity Without Context" significantly increases, making decryption far more challenging without additional information.
The Fundamentals of Encryption and Decryption
A foundational overview of how codes are made and broken.
Encryption is the process of converting a readable message (plaintext) into an unreadable form (ciphertext) to prevent unauthorized access. Decryption is the reverse process, transforming the ciphertext back into its original plaintext. Both processes rely on an algorithm (the cipher) and often a secret piece of information (the key).
This video provides an excellent introduction to basic ciphers, demonstrating how even simple alphabet ciphers can be used for encoding and decoding secret messages. It highlights the fundamental concepts of substitution and the importance of a shared understanding of the cipher.
The strength of an encryption method depends on the complexity of its algorithm and the length and randomness of its key. Simple substitution ciphers, where one character is consistently replaced by another, are relatively easy to break using frequency analysis (observing which characters appear most often). More advanced ciphers, like polyalphabetic ciphers (e.g., Vigenere cipher, which uses multiple Caesar ciphers based on a keyword), make frequency analysis much harder.
Caesar Cipher: A Historical Perspective
The Caesar cipher is one of the oldest and simplest forms of encryption. It's a type of shift cipher where each letter in the plaintext is shifted a fixed number of positions down or up the alphabet. For example, with a shift of 3, 'A' becomes 'D', 'B' becomes 'E', and so on. While not directly a number-based cipher in its traditional form, its mathematical principle (addition modulo 26) is fundamental to many other numeric encryption schemes.
A visual representation of the Caesar cipher, showing how letters are shifted by a fixed number of positions to encrypt a message.
Conclusion: The Art of Decryption Requires Context
Without knowing the specific cipher used, decrypting your numerical sequence remains a speculative task. The numbers provided do not neatly align with a single, simple number-to-letter cipher like A1Z26. While an ASCII interpretation offers some plausible letter conversions, the presence of numbers outside the typical ASCII range for letters suggests a more complex or hybrid encoding. Successful decryption in such cases often relies on contextual clues, external information about the cipher, or the application of advanced cryptanalysis tools that can test multiple possibilities simultaneously. The world of cryptography is vast, and every encrypted message is a puzzle waiting for its specific key.
Recommended Further Exploration
- How to identify unknown ciphers when given an encrypted message?
- What are some advanced number-based ciphers and their decryption methods?
- How does frequency analysis aid in breaking various types of ciphers?
- Explore the principles of modular arithmetic and its applications in encryption.
References
Frequently Asked Questions
Last updated May 21, 2025