Comprehensive Guide to Solving Quadratic Equations Using Python

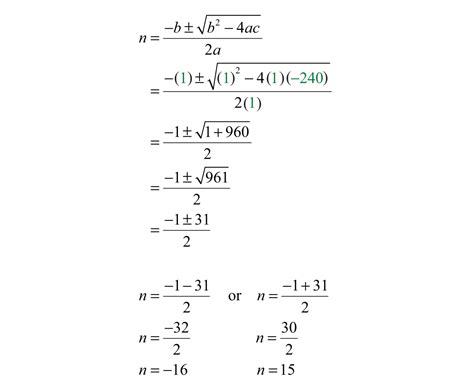
Introduction

Quadratic equations are fundamental in algebra, representing a wide range of real-world phenomena from projectile motion to financial forecasting. A quadratic equation is typically expressed in the form:

$$ ax^2 + bx + c = 0 $$

where a, b, and c are coefficients with a ≠ 0, and x represents the unknown variable. Solving this equation involves finding the values of x that satisfy the equation, known as the roots or solutions.

This guide provides an in-depth exploration of solving quadratic equations using Python, encompassing various implementations, error handling, and best practices to ensure robustness and efficiency in your programs.

Understanding the Quadratic Formula

The quadratic formula offers a systematic method to find the roots of any quadratic equation:

$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$

The expression under the square root,

$$ \Delta = b^2 - 4ac $$

is known as the discriminant. The discriminant determines the nature of the roots:

• If Δ > 0: Two distinct real roots.
• If Δ = 0: One real repeated root.
• If Δ < 0: Two complex conjugate roots.

Implementing the Quadratic Formula in Python

Python provides powerful libraries such as math and cmath to handle mathematical operations, including those involving complex numbers. Below, we explore various implementations to solve quadratic equations effectively.

1. Basic Implementation Using cmath

The cmath module in Python is designed to handle complex mathematical operations, making it ideal for solving quadratic equations, especially when dealing with complex roots.

a. Step-by-Step Code Explanation

Here is a straightforward Python function to solve quadratic equations:

import cmath

def solve_quadratic(a, b, c):
    """
    Solves the quadratic equation ax^2 + bx + c = 0
    Returns the roots, which can be real or complex numbers.
    """
    # Calculate the discriminant
    d = (b**2) - (4*a*c)
    
    # Calculate the two solutions
    sol1 = (-b - cmath.sqrt(d)) / (2*a)
    sol2 = (-b + cmath.sqrt(d)) / (2*a)
    
    return sol1, sol2

# Example usage
a = 1
b = 5
c = 6

sol1, sol2 = solve_quadratic(a, b, c)
print(f'The solutions are {sol1} and {sol2}')
  

This code performs the following steps:

• Calculate the Discriminant: Determines the nature of the roots.
• Compute the Roots: Uses the quadratic formula to find the solutions.
• Handle Complex Numbers: The cmath.sqrt() function ensures that even if the discriminant is negative, the roots are computed as complex numbers.

2. Enhanced Implementation with Error Handling

To create a more robust solution, it's essential to handle potential errors, such as cases where the coefficient a is zero, which would invalidate the quadratic equation.

a. Comprehensive Python Code

import cmath

def solve_quadratic(a, b, c):
    """
    Solves the quadratic equation ax^2 + bx + c = 0
    Returns a tuple containing the two roots and their nature.
    """
    if a == 0:
        raise ValueError("Coefficient 'a' cannot be zero for a quadratic equation.")
    
    # Calculate the discriminant
    discriminant = b**2 - 4*a*c
    
    # Calculate the two solutions
    sol1 = (-b - cmath.sqrt(discriminant)) / (2*a)
    sol2 = (-b + cmath.sqrt(discriminant)) / (2*a)
    
    # Determine the nature of the roots
    if discriminant > 0:
        nature = "Real and distinct roots"
    elif discriminant == 0:
        nature = "Real and repeated roots"
    else:
        nature = "Complex conjugate roots"
    
    return (sol1, sol2), nature

def main():
    print("Quadratic Equation Solver")
    print("Equation format: ax^2 + bx + c = 0")
    
    try:
        a = float(input("Enter coefficient a (non-zero): "))
        b = float(input("Enter coefficient b: "))
        c = float(input("Enter coefficient c: "))
        
        roots, nature = solve_quadratic(a, b, c)
        
        print("\nThe roots of the equation are:")
        print(f"Root 1: {roots[0]}")
        print(f"Root 2: {roots[1]}")
        print(f"Root nature: {nature}")
    
    except ValueError as ve:
        print(f"Error: {ve}")
    except Exception as e:
        print(f"An unexpected error occurred: {e}")

if __name__ == "__main__":
    main()
  

Key Features:

• Error Handling: Checks if coefficient a is zero and raises an appropriate error.
• Determining Root Nature: Based on the discriminant, it identifies whether the roots are real or complex.
• User Interaction: Prompts the user to input coefficients, enhancing usability.
• Clean Output: Clearly displays the roots and their nature.

3. Object-Oriented Approach

Leveraging Object-Oriented Programming (OOP) principles can lead to more organized and maintainable code, especially for more complex applications.

a. QuadraticEquation Class Implementation

import cmath

class QuadraticEquation:
    def __init__(self, a, b, c):
        if a == 0:
            raise ValueError("Coefficient 'a' must be non-zero for a quadratic equation.")
        self.a = a
        self.b = b
        self.c = c
        self.discriminant = self.b**2 - 4*self.a*self.c
    
    def calculate_roots(self):
        root1 = (-self.b + cmath.sqrt(self.discriminant)) / (2*self.a)
        root2 = (-self.b - cmath.sqrt(self.discriminant)) / (2*self.a)
        return root1, root2
    
    def nature_of_roots(self):
        if self.discriminant > 0:
            return "Two distinct real roots."
        elif self.discriminant == 0:
            return "One real repeated root."
        else:
            return "Two complex conjugate roots."

def main():
    print("Quadratic Equation Solver (OOP Approach)")
    print("Equation format: ax^2 + bx + c = 0")
    
    try:
        a = float(input("Enter coefficient a (non-zero): "))
        b = float(input("Enter coefficient b: "))
        c = float(input("Enter coefficient c: "))
        
        equation = QuadraticEquation(a, b, c)
        roots = equation.calculate_roots()
        nature = equation.nature_of_roots()
        
        print("\nThe roots of the equation are:")
        print(f"Root 1: {roots[0]}")
        print(f"Root 2: {roots[1]}")
        print(f"Root nature: {nature}")
    
    except ValueError as ve:
        print(f"Error: {ve}")
    except Exception as e:
        print(f"An unexpected error occurred: {e}")

if __name__ == "__main__":
    main()
  

Advantages of the OOP Approach:

• Modularity: Encapsulates related functionalities within a class.
• Reusability: The QuadraticEquation class can be easily reused in different parts of a larger application.
• Maintainability: Simplifies future enhancements and debugging.

4. Handling User Input and Providing User-Friendly Output

Creating an interactive program enhances user experience. Below is an implementation that guides the user through input and provides clear, formatted results.

import cmath

def solve_quadratic(a, b, c):
    """
    Solves the quadratic equation and returns the roots along with their nature.
    """
    if a == 0:
        raise ValueError("Coefficient 'a' cannot be zero for a quadratic equation.")
    
    discriminant = b**2 - 4*a*c
    sol1 = (-b + cmath.sqrt(discriminant)) / (2*a)
    sol2 = (-b - cmath.sqrt(discriminant)) / (2*a)
    
    if discriminant > 0:
        nature = "Real and distinct roots"
    elif discriminant == 0:
        nature = "Real and repeated roots"
    else:
        nature = "Complex conjugate roots"
    
    return (sol1, sol2), nature

def main():
    print("Welcome to the Quadratic Equation Solver!")
    print("Please enter the coefficients for the equation ax^2 + bx + c = 0.")
    
    try:
        a = float(input("Enter coefficient a (non-zero): "))
        b = float(input("Enter coefficient b: "))
        c = float(input("Enter coefficient c: "))
        
        roots, nature = solve_quadratic(a, b, c)
        
        print("\n--- Results ---")
        print(f"The roots of the equation {a}x² + {b}x + {c} = 0 are:")
        print(f"Root 1: {roots[0]}")
        print(f"Root 2: {roots[1]}")
        print(f"Nature of roots: {nature}")
    
    except ValueError as ve:
        print(f"Input Error: {ve}")
    except Exception as e:
        print(f"An unexpected error occurred: {e}")

if __name__ == "__main__":
    main()
  

Features:

• Interactive Prompts: Guides the user to input coefficients.
• Formatted Output: Clearly displays the equation and its roots.
• Error Messages: Provides informative error messages for invalid inputs.

5. Sample Outputs

a. Two Distinct Real Roots

Quadratic Equation Solver
Equation format: ax^2 + bx + c = 0
Enter coefficient a (non-zero): 1
Enter coefficient b: -3
Enter coefficient c: 2

The roots of the equation are:
Root 1: (2+0j)
Root 2: (1+0j)
Root nature: Real and distinct roots
  

b. One Real Repeated Root

Quadratic Equation Solver
Equation format: ax^2 + bx + c = 0
Enter coefficient a (non-zero): 1
Enter coefficient b: 2
Enter coefficient c: 1

The roots of the equation are:
Root 1: (-1+0j)
Root 2: (-1+0j)
Root nature: Real and repeated roots
  

c. Two Complex Conjugate Roots

Quadratic Equation Solver
Equation format: ax^2 + bx + c = 0
Enter coefficient a (non-zero): 1
Enter coefficient b: 0
Enter coefficient c: 1

The roots of the equation are:
Root 1: 1j
Root 2: -1j
Root nature: Complex conjugate roots
  

6. Best Practices and Enhancements

To further refine your quadratic equation solver, consider the following enhancements:

• Input Validation: Ensure that all inputs are valid numbers and handle unexpected input types gracefully.
• Modular Code: Break down the code into smaller, reusable functions or classes to enhance readability and maintainability.
• Documentation: Provide clear docstrings and comments to explain the purpose and functionality of each part of the code.
• Extended Functionality: Incorporate features such as plotting the quadratic curve or analyzing the vertex.
• Unit Testing: Implement unit tests to verify the correctness of your functions under various scenarios.

Conclusion

Solving quadratic equations is a quintessential aspect of algebra, and Python offers versatile tools to implement solutions efficiently. By understanding the mathematical underpinnings and leveraging Python's math and cmath modules, you can create robust programs capable of handling a wide range of scenarios, including real and complex roots.

Whether you opt for a procedural approach or embrace Object-Oriented Programming, the key lies in writing clear, maintainable, and well-documented code. Incorporating best practices such as error handling and user-friendly interactions further elevates the quality and usability of your quadratic equation solver.

For more detailed tutorials and examples, you can explore reputable resources such as Programiz, GeeksforGeeks, and Python Mania.

Empower yourself with these tools and techniques to tackle not only quadratic equations but also a broader spectrum of mathematical challenges using Python.