Understanding Euler's Number (e)

A Deep Dive into the Mathematical Constant e

Key Takeaways

• Fundamental Definition: Euler's number e is defined as the limit of (1 + 1/n)^n as n approaches infinity, approximately equal to 2.71828.
• Mathematical Significance: e is the base of natural logarithms and plays a critical role in calculus, particularly in exponential growth and decay models.
• Wide-ranging Applications: Beyond pure mathematics, e is essential in fields such as finance for compound interest calculations, physics for modeling natural phenomena, and engineering for describing oscillatory systems.

---

Introduction to Euler's Number (e)

Euler's number, commonly denoted by the letter e, is one of the most important constants in mathematics. With an approximate value of 2.718281828459045, e is an irrational and transcendental number, meaning it cannot be expressed as a simple fraction and is not a root of any non-zero polynomial equation with rational coefficients. The constant e serves as the base of natural logarithms and is deeply embedded in various branches of mathematics, including calculus, complex analysis, and number theory.

Mathematical Definitions and Representations

Limit Definition

One of the most fundamental definitions of e is through the concept of limits in calculus. Specifically, e is defined as the limit of the expression (1 + 1/n)^n as n approaches infinity:

$$ e = \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n $$

This definition arises naturally when studying compound interest, where n represents the number of compounding periods. As n increases, the expression converges to e, illustrating the principle of continuous compounding.

Infinite Series Representation

Euler's number can also be expressed as an infinite series. The most common series representation is:

$$ e = \sum_{n=0}^{\infty} \frac{1}{n!} = 1 + \frac{1}{1} + \frac{1}{2} + \frac{1}{6} + \frac{1}{24} + \cdots $$

Here, n! denotes the factorial of n, and the series converges rapidly to the value of e. This representation is particularly useful in calculus and analysis, facilitating the computation of e to a high degree of precision.

Euler's Formula in Complex Analysis

Euler's number plays a pivotal role in complex analysis through Euler's formula, which establishes a profound connection between exponential functions and trigonometric functions:

$$ e^{ix} = \cos(x) + i\sin(x) $$

Where:

• i is the imaginary unit, satisfying i² = -1.
• x is a real number representing an angle in radians.

This formula not only bridges exponential and trigonometric functions but also leads to Euler's identity when x is π:

$$ e^{i\pi} + 1 = 0 $$

Euler's identity is celebrated for its mathematical beauty, combining five of the most important numbers in mathematics: 0, 1, e, i, and π.

Properties of Euler's Number

Irrationality

Euler's number e is an irrational number, meaning it cannot be expressed as a fraction of two integers. This was proven by the Swiss mathematician Johann Heinrich Lambert in 1768. The decimal representation of e is non-terminating and non-repeating, which is a hallmark of irrational numbers.

Transcendence

Beyond being irrational, e is also transcendental. A transcendental number is not a root of any non-zero polynomial equation with rational coefficients. This property was established by Charles Hermite in 1873, further cementing e's unique position in the realm of mathematics.

Uniqueness as the Base of Natural Logarithms

One of the defining features of e is its role as the base of natural logarithms. The natural logarithm, denoted as ln(x), is the inverse function of the exponential function with base e. This relationship simplifies many mathematical operations, particularly in calculus, where the derivative of ln(x) is 1/x, and the derivative of e^x is e^x.

Applications of Euler's Number

Calculus and Differential Equations

In calculus, e is indispensable for understanding exponential growth and decay processes. The function e^x is unique in that it is its own derivative and integral, making it a natural choice for solving differential equations that model real-world phenomena such as population dynamics, radioactive decay, and heat transfer.

Exponential Growth and Decay

Exponential functions involving e are used to model situations where a quantity grows or decays at a rate proportional to its current value. For example, the population of a species might grow exponentially in an ideal environment without resource constraints, while the decay of a radioactive substance follows an exponential decay model.

Finance and Compound Interest

In finance, e is fundamental in the calculation of continuous compound interest. Unlike simple or periodic compounding, continuous compounding assumes interest is being added instantaneously and continuously. The formula for continuous compounding is:

$$ A = P \cdot e^{rt} $$

Where:

• A is the amount of money accumulated after time t.
• P is the principal amount (initial investment).
• r is the annual interest rate (in decimal).
• t is the time the money is invested for.

Probability Theory and Statistics

In probability theory, e appears in the context of normal distributions and Poisson processes. For instance, the probability density function of the normal distribution incorporates e to describe the spread and likelihood of data points around the mean. Additionally, e arises in the formula for the Poisson distribution, which models the number of events occurring within a fixed interval of time or space.

Engineering and Physics

Euler's number is prevalent in various engineering and physics applications. In electrical engineering, e is used in the analysis of electrical circuits involving capacitors and inductors. In physics, e is essential in describing phenomena such as wave functions in quantum mechanics and the behavior of oscillatory systems.

Euler's Number in Complex Analysis

Euler's Formula Revisited

Euler's formula, e^{ix} = \cos(x) + i\sin(x), is a cornerstone of complex analysis. It establishes a profound link between exponential functions and trigonometric functions, enabling the representation of complex numbers in exponential form. This relationship simplifies many calculations involving complex exponentials and is fundamental in fields like electrical engineering, quantum physics, and applied mathematics.

Fourier Transforms

In the realm of signal processing, Euler's number is integral to Fourier transforms, which decompose functions into their constituent frequencies. The exponential terms in Fourier transforms, which involve e, facilitate the analysis and manipulation of signals in both time and frequency domains.

Visual Representation of Euler's Number

Graphing e^x

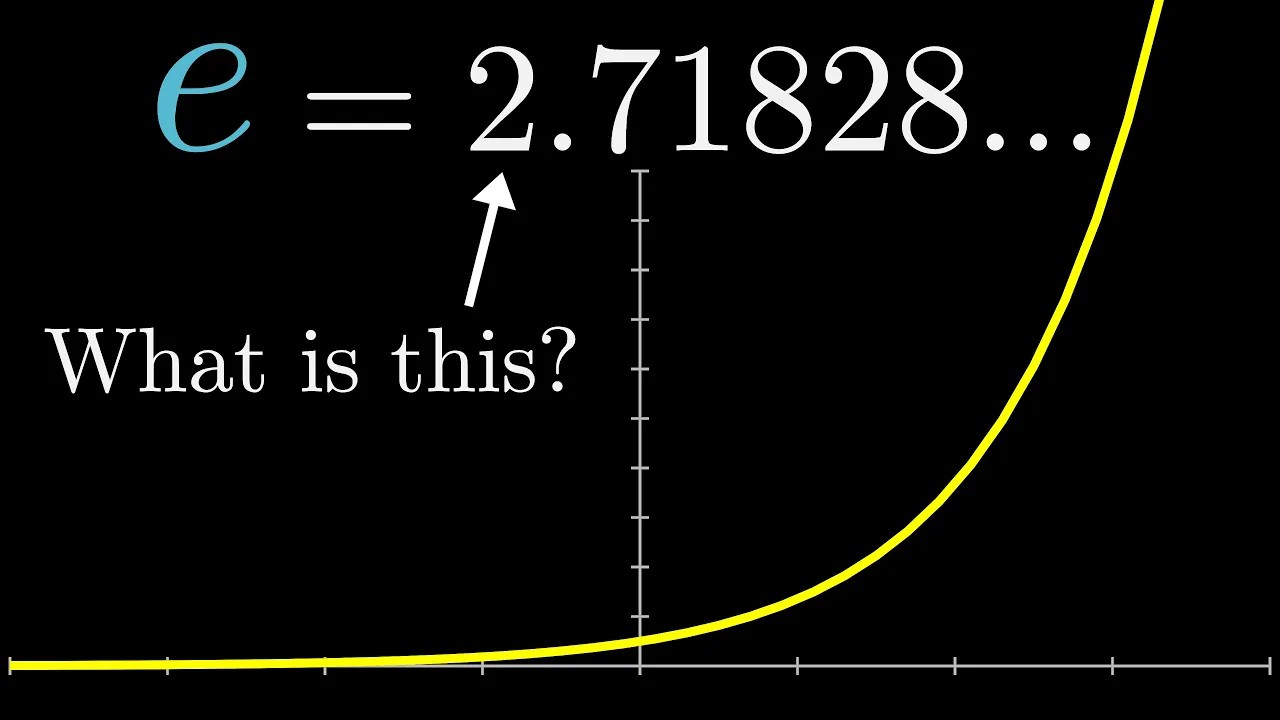
The exponential function e^x is characterized by its rapid growth and unique properties in calculus. When graphed, e^x starts at 1 when x=0 and increases steeply as x becomes positive. Conversely, as x becomes negative, e^x approaches zero but never touches the x-axis, illustrating its asymptotic nature.

Table of e^x Values

x	e^x
-2	0.1353
-1	0.3679
0	1
1	2.7183
2	7.3891
3	20.0855

Historical Context and Discovery

Origins of e

The constant e was first discovered by the Swiss mathematician Jacob Bernoulli in 1683 while studying compound interest. Bernoulli was interested in understanding the behavior of interest rates compounded more frequently, leading to the formulation of the limit that defines e. The number was later named after the prolific mathematician Leonhard Euler, who made significant contributions to its formalization and application.

Euler's Contributions

Leonhard Euler was instrumental in the development and popularization of the constant e. His work in establishing the various representations of e, including its infinite series and its role in complex analysis through Euler's formula, solidified its importance in mathematics. Euler's extensive research and publications ensured that e became a fundamental constant in mathematical education and research.

Practical Applications of e

Compound Interest Calculations

In finance, e is used to calculate continuous compound interest, which assumes that interest is being added an infinite number of times per year. The formula:

$$ A = P \cdot e^{rt} $$

allows investors to determine the future value of an investment with continuous compounding, where:

• A = Future value
• P = Principal investment
• r = Annual interest rate
• t = Time in years

Population Growth Modeling

Biologists and demographers use e to model population growth under ideal conditions. The exponential growth model assumes that the population grows at a rate proportional to its current size, leading to the equation:

$$ P(t) = P_0 \cdot e^{rt} $$

Where:

• P(t) = Population at time t
• P₀ = Initial population
• r = Growth rate
• t = Time

Radioactive Decay

In physics, e is used to describe the decay of radioactive substances. The decay model follows the equation:

$$ N(t) = N_0 \cdot e^{-\lambda t} $$

Where:

• N(t) = Quantity remaining at time t
• N₀ = Initial quantity
• λ = Decay constant
• t = Time

Euler's Number in Advanced Mathematics

Differential Equations

Euler's number is critical in solving both ordinary and partial differential equations. Its unique property of being its own derivative simplifies the process of finding solutions to equations that model physical systems.

Complex Analysis

In complex analysis, e facilitates the study of complex functions. Euler's formula, which relates e to trigonometric functions, is foundational in understanding oscillatory behavior and waveforms in the complex plane.

Number Theory

While e is primarily associated with analysis, it also has implications in number theory, particularly in the study of transcendental numbers and the distribution of prime numbers.

Conclusion

Euler's number e is a cornerstone of modern mathematics, integral to a wide array of mathematical concepts and applications. Its unique properties as an irrational and transcendental number, combined with its foundational role in calculus, complex analysis, and various applied fields, make e an indispensable constant in both theoretical and practical contexts. From modeling natural growth processes to solving complex differential equations, e continues to be a subject of profound importance and utility in advancing mathematical understanding and innovation.

References