Mastering the Java PriorityQueue: Implementation and Real-World Applications

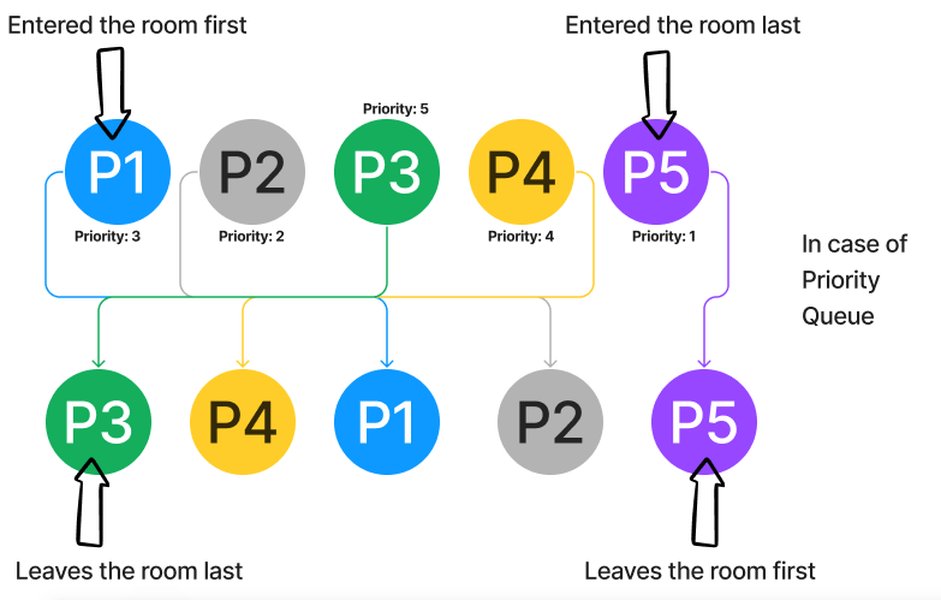
The Java PriorityQueue is a foundational data structure within the java.util package, designed to manage elements based on their inherent priority rather than the traditional First-In-First-Out (FIFO) order of a standard queue. Unlike regular queues where elements are processed strictly by their insertion order, a PriorityQueue ensures that the element with the highest priority is always at the front, ready for retrieval. This behavior makes it invaluable for scenarios where the processing order is critical and depends on specific criteria.

Internally, the PriorityQueue in Java is implemented using a priority heap, specifically a min-heap by default. This heap-based implementation allows for efficient insertion (enqueuing) and removal (dequeuing) operations, typically achieving O(log N) time complexity, where N is the number of elements in the queue. This logarithmic time complexity ensures that even with a large number of elements, the performance remains robust. The capacity of a PriorityQueue is unbounded and automatically resizes as elements are added, further simplifying its use.

Key Highlights of Java's PriorityQueue

Priority-Based Ordering: Elements are retrieved based on their priority, not insertion order. By default, it acts as a min-priority queue, meaning the smallest element (according to natural ordering or a custom comparator) has the highest priority.
Heap-Based Implementation: The underlying data structure is a binary heap, which optimizes the performance of insertion and removal operations to logarithmic time complexity.
Versatile Ordering Mechanisms: You can define element priority either through their natural ordering (if elements implement Comparable) or by providing a custom Comparator, offering significant flexibility for diverse use cases.

Understanding the Core Mechanism

How PriorityQueue Differs from Standard Queues

A standard queue, like those implemented by LinkedList or ArrayDeque, adheres to the First-In-First-Out (FIFO) principle. This means the element added first is the first one to be removed. Consider a line at a supermarket: the person who joined the queue first is served first. In contrast, a PriorityQueue operates more like an emergency room. While patients arrive sequentially, they are treated based on the severity of their condition (priority), not necessarily their arrival time. The most critical patient is always attended to first.

This fundamental difference makes the PriorityQueue indispensable for scenarios where the "next" item to be processed isn't simply the oldest, but the one deemed most important or urgent. The internal heap structure automatically rearranges itself to ensure the highest priority element is always at the "head" of the queue, making its retrieval highly efficient.

Internal Implementation: The Priority Heap

The Java PriorityQueue relies on a min-heap data structure. A min-heap is a complete binary tree where the value of each node is less than or equal to the value of its children. This property ensures that the smallest element is always at the root of the tree, which corresponds to the head of the PriorityQueue. When an element is added or removed, the heap properties are maintained through "heapify" operations, which involve comparisons and swaps, leading to the O(log N) time complexity for these operations.

For example, if you add an element to a PriorityQueue, it's initially placed at the end of the internal array that represents the heap. Then, it "bubbles up" by repeatedly swapping with its parent if its priority is higher (i.e., its value is smaller in a min-heap) until it reaches its correct position. Similarly, when the highest priority element (root) is removed, the last element in the heap is moved to the root, and then it "bubbles down" by repeatedly swapping with its smaller child until the heap property is restored.

Diagram illustrating a min-heap, the underlying structure of Java's PriorityQueue.

An illustration of a min-heap, which serves as the internal mechanism for Java's PriorityQueue, ensuring the smallest element is always at the root.

Practical Java PriorityQueue Implementation

Basic Usage with Natural Ordering

By default, Java's PriorityQueue orders elements according to their natural ordering. This means if you store Integer, String, or other Comparable objects, they will be ordered in ascending order. The "least" element (smallest value) will have the highest priority.

import java.util.PriorityQueue;

public class BasicPriorityQueueExample {
    public static void main(String[] args) {
        // Create a PriorityQueue of Integers (natural ordering - min-heap)
        PriorityQueue<Integer> numbers = new PriorityQueue<>();

        // Add elements
        numbers.add(10);
        numbers.add(2);
        numbers.add(7);
        numbers.offer(5); // offer() is similar to add() for PriorityQueue

        System.out.println("PriorityQueue elements (insertion order not guaranteed): " + numbers);

        // Retrieve and remove elements (elements are removed in ascending order)
        System.out.println("Polling elements:");
        while (!numbers.isEmpty()) {
            System.out.println("  " + numbers.poll()); // poll() retrieves and removes the head
        }
        System.out.println("PriorityQueue after polling: " + numbers);
    }
}

Custom Ordering with Comparator

For custom objects or to define a specific ordering (e.g., descending order for integers), you can provide a Comparator during the PriorityQueue's construction. This allows you to precisely control which elements are considered "higher priority."

import java.util.Comparator;
import java.util.PriorityQueue;

public class CustomPriorityQueueExample {

    // Custom class to demonstrate complex object prioritization
    static class Task implements Comparable<Task> {
        String name;
        int priorityLevel; // Lower number means higher priority

        public Task(String name, int priorityLevel) {
            this.name = name;
            this.priorityLevel = priorityLevel;
        }

        // Natural ordering based on priorityLevel (ascending)
        @Override
        public int compareTo(Task other) {
            return Integer.compare(this.priorityLevel, other.priorityLevel);
        }

        @Override
        public String toString() {
            return "Task{" + "name='" + name + '\'' + ", priority=" + priorityLevel + '}';
        }
    }

    public static void main(String[] args) {
        // Example 1: Custom ordering for Integers (descending order - max-heap behavior)
        PriorityQueue<Integer> maxHeapNumbers = new PriorityQueue<>(Comparator.reverseOrder());
        maxHeapNumbers.add(10);
        maxHeapNumbers.add(2);
        maxHeapNumbers.add(7);
        maxHeapNumbers.offer(5);

        System.out.println("Max-Heap like PriorityQueue elements: " + maxHeapNumbers);
        System.out.println("Polling elements from max-heap:");
        while (!maxHeapNumbers.isEmpty()) {
            System.out.println("  " + maxHeapNumbers.poll());
        }

        System.out.println("\n-----------------------------------\n");

        // Example 2: PriorityQueue with custom objects using their natural ordering (compareTo)
        PriorityQueue<Task> tasks = new PriorityQueue<>(); // Uses Task's compareTo()
        tasks.add(new Task("Emergency Fix", 1));
        tasks.add(new Task("Minor Bug", 3));
        tasks.add(new Task("Feature Development", 2));
        tasks.add(new Task("Critical Outage", 0));

        System.out.println("Tasks in order of priority (lower number = higher priority):");
        while (!tasks.isEmpty()) {
            System.out.println("  " + tasks.poll());
        }

        System.out.println("\n-----------------------------------\n");

        // Example 3: PriorityQueue with custom objects using an external Comparator
        // Let's say we want to prioritize tasks by name length (shorter names first)
        Comparator<Task> nameLengthComparator = Comparator.comparingInt(t -> t.name.length());
        PriorityQueue<Task> tasksByNameLength = new PriorityQueue<>(nameLengthComparator);
        tasksByNameLength.add(new Task("Emergency Fix", 1));
        tasksByNameLength.add(new Task("Minor Bug", 3));
        tasksByNameLength.add(new Task("Feature Development", 2));
        tasksByNameLength.add(new Task("Critical Outage", 0));
        tasksByNameLength.add(new Task("Bug", 4)); // Shorter name

        System.out.println("Tasks ordered by name length (shortest name = highest priority):");
        while (!tasksByNameLength.isEmpty()) {
            System.out.println("  " + tasksByNameLength.poll());
        }
    }
}

The ability to define custom ordering via Comparator makes PriorityQueue extremely flexible, allowing it to manage complex data types based on various criteria.

Common PriorityQueue Operations and Their Characteristics

The PriorityQueue class provides a set of methods for managing its elements. Understanding these operations and their time complexities is crucial for efficient application development.

This radar chart visualizes the performance and characteristics of key PriorityQueue operations. Each axis represents a specific attribute, with data points indicating the relative strength or complexity of the operation in that area. For instance, 'Efficiency (Avg)' represents the typical time complexity, 'Efficiency (Worst)' shows the maximum possible time complexity, 'Memory Usage' indicates resource consumption, 'Ease of Use' reflects the simplicity of the API, and 'Concurrency Safety' denotes its behavior in multi-threaded environments. Higher values further from the center generally indicate better performance or desirable traits, though for complexity, a lower value is better. The chart underscores the PriorityQueue's strength in logarithmic time for adding and removing elements, while highlighting its non-thread-safe nature by default.

Key PriorityQueue Methods and Their Characteristics
Method	Description	Time Complexity	Return Value	Notes
`add(E e)`	Inserts the specified element into the queue.	\(O(\log n)\)	`boolean` (always `true` for `PriorityQueue`)	Throws `IllegalStateException` if capacity-restricted (not typical for `PriorityQueue`) or `NullPointerException` if `null` element.
`offer(E e)`	Inserts the specified element into the queue.	\(O(\log n)\)	`boolean` (always `true` for `PriorityQueue`)	Generally preferred over `add()` for queues, as it returns `false` instead of throwing an exception if insertion fails (though rarely fails for `PriorityQueue`).
`element()`	Retrieves, but does not remove, the head of this queue.	\(O(1)\)	`E` (the head)	Throws `NoSuchElementException` if the queue is empty.
`peek()`	Retrieves, but does not remove, the head of this queue.	\(O(1)\)	`E` (the head) or `null`	Returns `null` if the queue is empty, making it safer than `element()`.
`remove()`	Retrieves and removes the head of this queue.	\(O(\log n)\)	`E` (the head)	Throws `NoSuchElementException` if the queue is empty.
`poll()`	Retrieves and removes the head of this queue.	\(O(\log n)\)	`E` (the head) or `null`	Returns `null` if the queue is empty, making it safer than `remove()`.
`size()`	Returns the number of elements in this queue.	\(O(1)\)	`int`	Directly returns the size.
`contains(Object o)`	Returns `true` if this queue contains the specified element.	\(O(n)\)	`boolean`	May require iterating through elements in the worst case.
`clear()`	Removes all of the elements from this queue.	\(O(n)\)	`void`	Clears the queue.

Real-World Use Cases for PriorityQueue

The PriorityQueue is a versatile data structure with numerous applications in computer science and real-world scenarios where elements need to be processed based on their importance or urgency.

Task Scheduling in Operating Systems

In operating systems, tasks often have different priorities. A critical system process should run before a background user application. A PriorityQueue can effectively manage these tasks, always ensuring that the highest priority task gets CPU time first. This is a fundamental concept in real-time operating systems (RTOS) and general-purpose operating systems.

Illustration of various real-world applications of priority queues.

Diverse applications of priority queues range from network routing to event simulation, highlighting their versatility.

Event Simulation

In discrete event simulations, events occur at specific times and need to be processed in chronological order. A PriorityQueue can store future events, ordered by their timestamp. The simulation always processes the event with the earliest timestamp, then removes it and proceeds to the next. This ensures that the simulation progresses accurately based on time-ordered events.

Graph Algorithms

Many graph algorithms, such as Dijkstra's shortest path algorithm and Prim's minimum spanning tree algorithm, heavily rely on a PriorityQueue. In Dijkstra's algorithm, the queue stores vertices along with their tentative shortest distances from the source, always extracting the vertex with the smallest distance to explore next. In Prim's algorithm, it keeps track of edges to be considered, prioritized by weight, to build the minimum spanning tree.

// Pseudocode for Dijkstra's Algorithm using a PriorityQueue
// (Illustrative - not full Java implementation)

function Dijkstra(graph, startNode):
    distances = map from node to infinity
    distances[startNode] = 0

    priorityQueue = new PriorityQueue() // Stores (distance, node) pairs
    priorityQueue.add((0, startNode))

    while priorityQueue is not empty:
        currentDistance, currentNode = priorityQueue.poll()

        if currentDistance > distances[currentNode]:
            continue // Already found a shorter path

        for neighbor in graph.neighbors(currentNode):
            newDistance = currentDistance + graph.edgeWeight(currentNode, neighbor)
            if newDistance < distances[neighbor]:
                distances[neighbor] = newDistance
                priorityQueue.add((newDistance, neighbor))

    return distances

Huffman Coding

Huffman coding, a data compression algorithm, uses a PriorityQueue to build the optimal prefix code. It repeatedly extracts the two nodes with the smallest frequencies, combines them into a new parent node, and re-inserts the new node into the queue. This process continues until only one node (the root of the Huffman tree) remains.

Emergency Services Dispatch

Consider an emergency dispatch system (e.g., 911 or hospital emergency room). Calls or incoming patients are assigned a priority level based on urgency. A PriorityQueue ensures that the most critical emergencies are addressed first, regardless of when they were reported. This saves lives by optimizing resource allocation.

This video provides an excellent introduction to Priority Queues, illustrating their core concept and differentiating them from standard FIFO queues with a compelling real-world example of an emergency room, which perfectly encapsulates the priority-based processing that defines this data structure.

Finding K-th Smallest/Largest Element

A PriorityQueue can efficiently find the K-th smallest or largest element in a collection. For the K-th smallest, you maintain a max-heap of size K. For each new element, if it's smaller than the heap's maximum, you remove the max and insert the new element. The heap's max after processing all elements will be the K-th smallest. Similarly, for the K-th largest, you use a min-heap.

Considerations for Using PriorityQueue

Thread Safety

It's crucial to remember that the standard java.util.PriorityQueue is not thread-safe. If multiple threads need to access and modify the queue concurrently, you should use the thread-safe equivalent: java.util.concurrent.PriorityBlockingQueue. This class provides concurrent access guarantees and blocking operations, making it suitable for multi-threaded environments.

Null Elements and Non-Comparable Objects

The PriorityQueue does not permit null elements. Attempting to insert a null will result in a NullPointerException. Furthermore, if the PriorityQueue is using natural ordering, elements must implement the Comparable interface; otherwise, a ClassCastException will be thrown if non-comparable objects are inserted. When using a custom Comparator, this restriction applies to the types the comparator is designed to handle.

Frequently Asked Questions (FAQ)

What is the default ordering of a Java PriorityQueue?

By default, the Java PriorityQueue maintains a min-heap structure, meaning elements are ordered according to their natural ordering (ascending order). The element with the "least" value (e.g., smallest integer, alphabetically first string) is considered to have the highest priority and will be retrieved first.

Can I use a PriorityQueue with custom objects?

Yes, you can use a PriorityQueue with custom objects. Your custom class must either implement the Comparable interface (for natural ordering based on one of its properties) or you must provide a Comparator instance to the PriorityQueue's constructor to define a custom ordering logic.

What is the difference between add() and offer() methods in PriorityQueue?

For an unbounded PriorityQueue, add() and offer() behave identically, both inserting an element and returning true. However, in general queue implementations, add() throws an IllegalStateException if the queue is full, while offer() returns false. For PriorityQueue, offer() is often preferred due to its more generic contract adherence to the Queue interface.

Is PriorityQueue thread-safe?

No, java.util.PriorityQueue is not thread-safe. If you need a thread-safe priority queue for concurrent access in a multi-threaded environment, you should use java.util.concurrent.PriorityBlockingQueue.

What is the time complexity of common PriorityQueue operations?

Insertion (add(), offer()) and removal (poll(), remove()) operations have a time complexity of \(O(\log n)\), where \(n\) is the number of elements. Retrieval of the head element (peek(), element()) has a time complexity of \(O(1)\). The contains() method has a time complexity of \(O(n)\) in the worst case.

Conclusion

The Java PriorityQueue is a powerful and efficient data structure that deviates from the traditional FIFO queue by ordering elements based on priority. Its underlying heap implementation ensures logarithmic time complexity for critical insertion and deletion operations, making it highly suitable for applications requiring dynamic prioritization. From task scheduling and event simulation to complex graph algorithms and real-time emergency dispatch systems, the PriorityQueue provides a robust solution for managing ordered data effectively. Understanding its characteristics, including natural ordering, custom comparators, and thread safety considerations, empowers developers to leverage this utility to build highly optimized and responsive applications.