Understanding Linear Expansivity

A Comprehensive Exploration of Thermal Expansion in Materials

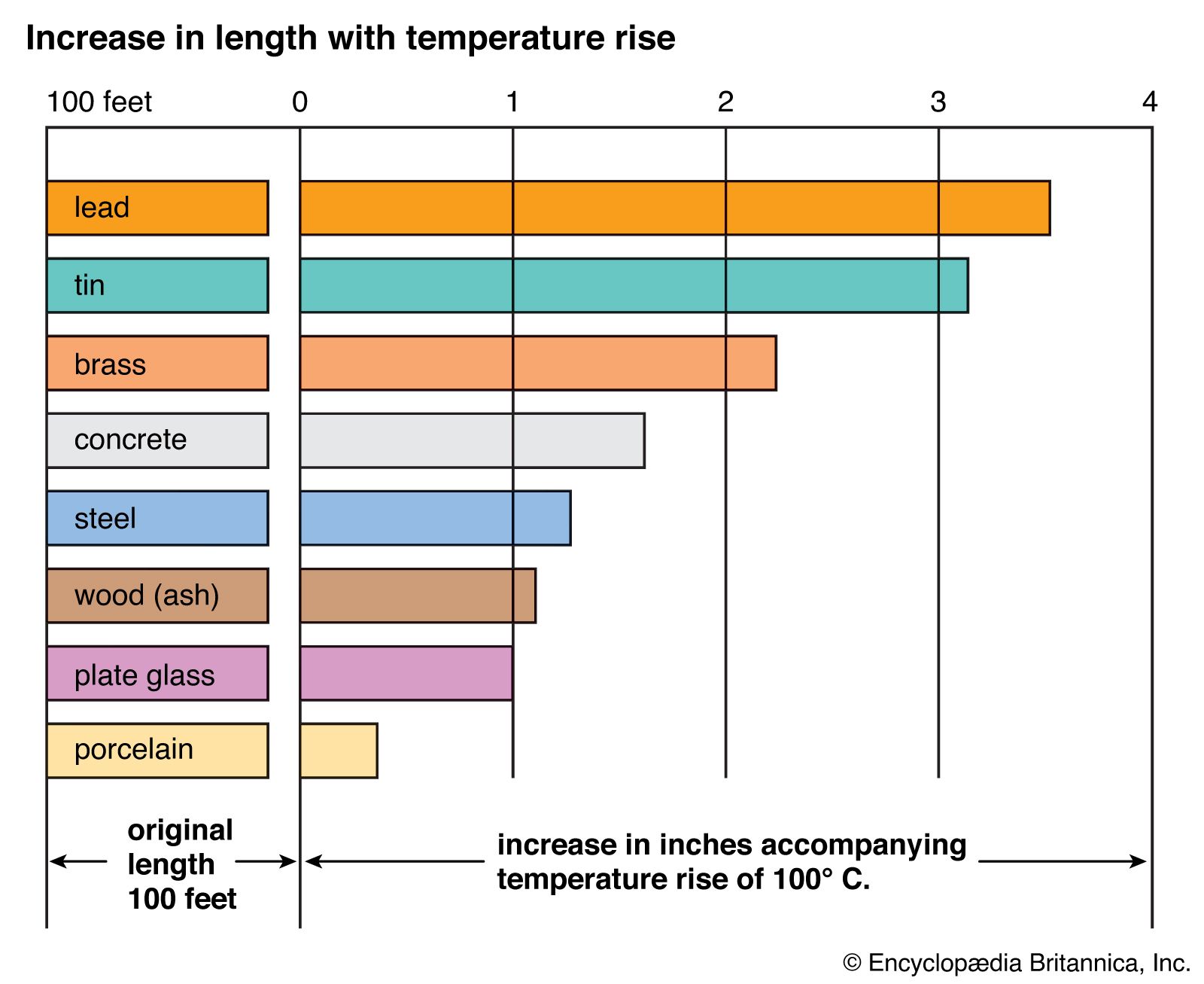
Key Takeaways

Coefficient of Linear Expansion (α): A fundamental property determining how materials respond to temperature changes.
Practical Applications: Essential in engineering disciplines to ensure structural integrity and functionality under varying temperatures.
Material Selection: Different materials exhibit varying linear expansivity, influencing their suitability for specific applications.

Introduction to Linear Expansivity

Linear expansivity, often referred to as linear thermal expansion, is a critical physical property that quantifies the change in length of a material in response to temperature variations. Understanding this property is paramount in materials science, engineering, and various applied fields to ensure the reliability and durability of structures and components subjected to thermal stresses.

Fundamental Concepts

Definition and Measurement

Linear expansivity is defined as the fractional change in length per unit length per degree change in temperature. Mathematically, it is represented by the coefficient of linear expansion (α), which can be expressed using the formula:

$$\alpha = \frac{\Delta L}{L_0 \cdot \Delta T}$$

Where:

ΔL = Change in length
L₀ = Original length
ΔT = Change in temperature

The units of α are typically expressed in per degree Celsius (°C⁻¹) or per Kelvin (K⁻¹). Accurate measurement of linear expansivity is essential for predicting how materials will behave under thermal fluctuations.

Mathematical Representation

The linear expansion of a material can be calculated using the equation:

$$\Delta L = \alpha \cdot L_0 \cdot \Delta T$$

This equation allows engineers and scientists to predict the change in dimensions of a material when subjected to a specific temperature change.

Factors Influencing Linear Expansivity

Material Composition

Different materials possess distinct values of α, influencing how they expand or contract with temperature changes. Metals, for instance, typically exhibit higher coefficients of linear expansion compared to ceramics or polymers. This variance is due to the differing atomic structures and bonding strengths within these materials.

Temperature Range

The linear expansivity of a material can vary over different temperature ranges. Some materials may display linear behavior only within a specific temperature interval, beyond which non-linear expansion occurs due to phase changes or other structural alterations.

Anisotropy

In anisotropic materials, the coefficient of linear expansion may differ along various axes. This property necessitates careful consideration in applications where directional thermal expansion could impact performance or structural integrity.

Practical Applications of Linear Expansivity

Engineering and Construction

Engineers must account for linear expansivity when designing structures like bridges, railways, and buildings. Thermal expansion joints are incorporated to accommodate the expansion and contraction of materials, preventing structural damage and ensuring longevity.

Precision Instruments

In the realm of precision engineering, materials with low thermal expansivity are preferred to maintain accuracy in instruments such as telescopes, microscopes, and measuring devices. Minimizing dimensional changes under temperature variations is crucial for the reliability of these instruments.

Manufacturing

Manufacturing processes often involve temperature variations, making it essential to select materials with appropriate linear expansivity to ensure dimensional stability and proper fit of components. For example, glassware and cookware are designed considering their expansion rates to prevent breakage and ensure functionality.

Calculating Linear Expansivity

Basic Calculation Example

Consider a metal rod with an original length of 1.0 meter at 20°C. If the temperature increases to 70°C (ΔT = 50°C) and the coefficient of linear expansion (α) is 1.2 × 10⁻⁵ °C⁻¹, the change in length (ΔL) can be calculated as:

ΔL = α × L₀ × ΔT
ΔL = 1.2 × 10⁻⁵ × 1.0 m × 50°C
ΔL = 0.0006 m or 0.6 mm

The rod expands by 0.6 millimeters with the temperature increase.

Advanced Calculation Example

For a more substantial example, consider a metal rod initially 18.02 meters long, expanding to 20.01 meters when heated from room temperature to 800°C. The change in temperature (ΔT) is 800°C.

First, calculate ΔL:

$$\Delta L = L_2 - L_1 = 20.01 \text{ m} - 18.02 \text{ m} = 1.99 \text{ m}$$

Then, determine α:

$$\alpha = \frac{\Delta L}{L_1 \cdot \Delta T} = \frac{1.99}{18.02 \times 800} \approx 0.00013804 \text{ K}^{-1}$$

Comparative Analysis of Materials

Coefficients of Linear Expansion for Common Materials

Material	Coefficient of Linear Expansion (α) [°C⁻¹]
Copper	16.5 × 10⁻⁶
Aluminum	23.1 × 10⁻⁶
Steel	12.0 × 10⁻⁶
Brass	19.0 × 10⁻⁶
Glass	9.0 × 10⁻⁶
Polyethylene	200 × 10⁻⁶

Implications of Material Choice

The table above highlights the varying coefficients of linear expansion across different materials. For applications requiring minimal thermal expansion, materials like glass and steel are preferable due to their lower α values. Conversely, materials like polyethylene exhibit high thermal expansivity, making them suitable for applications where flexibility under temperature changes is desired.

Applications and Design Considerations

Infrastructure and Civil Engineering

In the construction of bridges, highways, and buildings, thermal expansion can lead to significant structural stresses. Incorporating expansion joints is a common design practice to absorb the expansion and contraction of materials, thereby preventing cracks, warping, or other forms of structural damage.

Mechanical Engineering

Engine components such as pistons, engine blocks, and turbine blades experience temperature fluctuations during operation. Understanding their linear expansivity is crucial to ensure proper clearance, prevent seizure, and maintain performance under varying thermal conditions.

Electronics and Precision Instruments

Electronic devices and precision instruments require materials with predictable thermal expansion properties to maintain accuracy and functionality. Materials with low linear expansivity are selected to minimize dimensional changes that could affect the alignment and calibration of sensitive components.

Managing Thermal Expansion

Use of Expansion Joints

Expansion joints are engineered gaps integrated into structures to accommodate the expansion and contraction of building materials. These joints prevent the accumulation of thermal stresses that could lead to structural failure.

Material Selection and Composite Design

When designing composite materials or selecting materials for specific applications, engineers consider the linear expansivity of each component to ensure compatibility and prevent differential expansion. This approach helps maintain structural integrity and performance across temperature variations.

Temperature Control Systems

Implementing effective temperature control systems can mitigate the effects of thermal expansion. By maintaining a stable operating temperature, the dimensional changes of materials can be minimized, enhancing the reliability and longevity of the system.

Challenges and Considerations

Anisotropic Expansion

In anisotropic materials, linear expansivity varies with direction. This property complicates design considerations, requiring detailed analysis to predict and manage differential expansions that could induce stress or deformation.

Extreme Temperature Conditions

At extreme temperatures, materials may exhibit non-linear expansion behavior or undergo phase changes, altering their linear expansivity. Understanding these behaviors is essential for designing systems that operate reliably under such conditions.

Composite Materials

Combining materials with differing linear expansivities in composites introduces challenges in managing overall thermal expansion. Engineers must carefully design composites to balance the expansion characteristics of each component, preventing delamination or structural weakness.

Future Directions and Innovations

Smart Materials

Advancements in materials science are leading to the development of smart materials that can actively adjust their thermal expansion properties in response to environmental changes. These materials hold promise for applications requiring dynamic control of dimensional stability.

Nanotechnology

Nanotechnology offers opportunities to engineer materials at the molecular level, enabling precise control over linear expansivity. Such control can lead to the creation of materials with tailored thermal expansion properties for specialized applications.

Eco-friendly Materials

With a growing emphasis on sustainability, research is focusing on developing eco-friendly materials that maintain favorable thermal expansion characteristics while minimizing environmental impact. These materials aim to provide both performance and sustainability in various applications.

Conclusion

Linear expansivity is a pivotal property in the realm of materials science and engineering, influencing the behavior and performance of materials under temperature variations. Understanding the coefficient of linear expansion enables the design and implementation of structures and components that can withstand thermal stresses, ensuring longevity and functionality. As technology advances, the ability to manipulate and control linear expansivity continues to evolve, opening new avenues for innovation and application across diverse industries.