Understanding the MD Function

An exploration of the many facets of "MD function" across disciplines

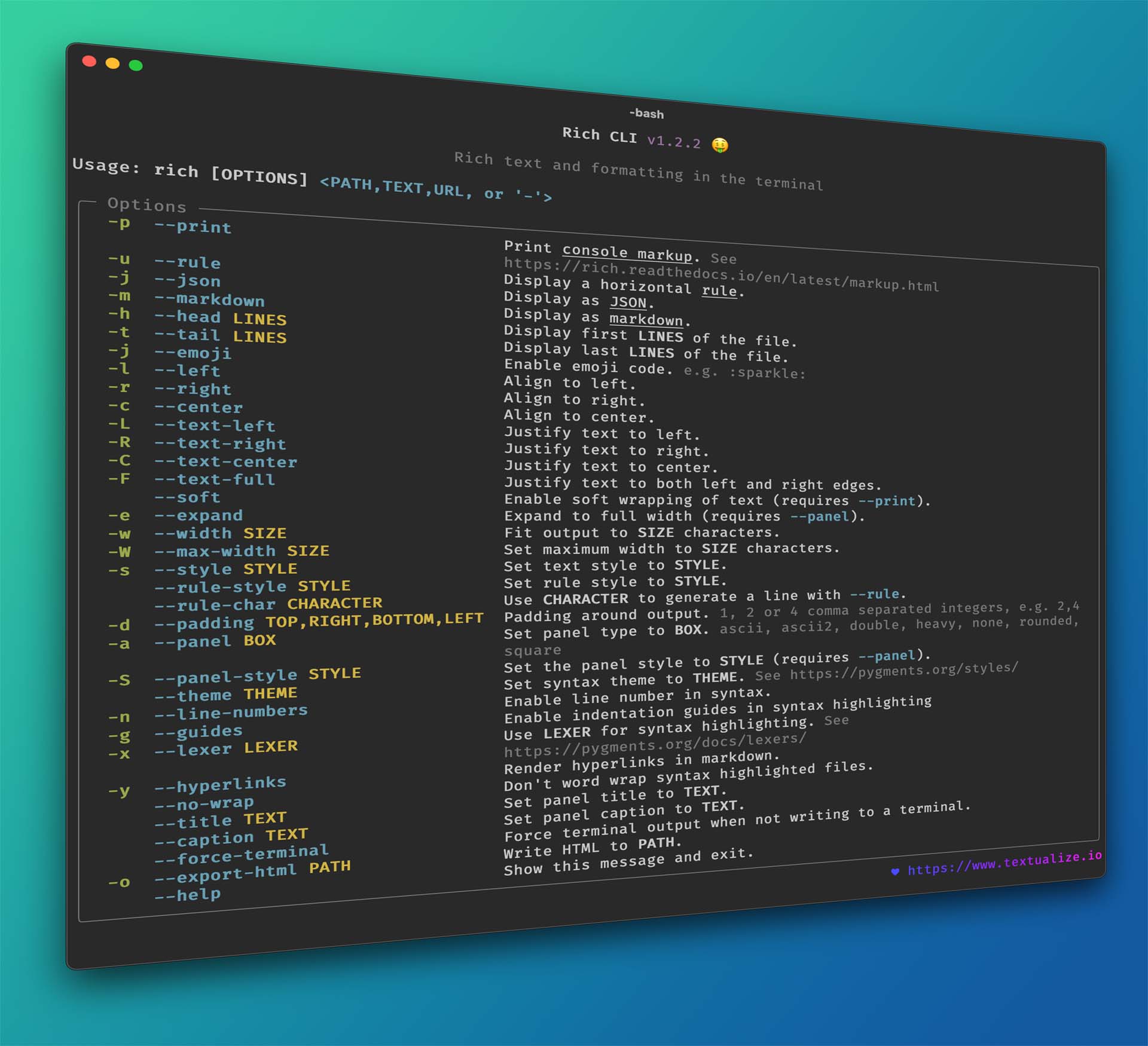
programmer using markdown and command line

Key Highlights

Multidisciplinary Terminology: "MD function" spans areas including programming, cryptography, medicine, and command-line operations.
Contextual Definitions: Its meaning is highly dependent on context—for instance, whether it refers to Markdown rendering, message digest operations, or even mathematical and statistical functions.
Practical Applications: Each interpretation of MD has distinct practical uses, from formatting documents to verifying data integrity and organizing system files.

Overview of the MD Function

The term "MD function" is a versatile expression utilized in various fields. Given its broad application, an exploration of its functions entails understanding its usage in several distinct environments. Whether it involves rendering Markdown text to a formatted output, creating directories in a command-line interface, verifying data integrity through cryptographic hash functions, or even assessing performance in independent component analysis (ICA), the MD function has wide-ranging implications.

1. MD in Programming and Documentation

Markdown Rendering

In many modern programming environments, the abbreviation "MD" is commonly linked to Markdown—a lightweight markup language that allows users to write formatted text using plain text. One of its most significant roles is in the conversion of Markdown text into HTML. This is particularly useful in dynamically generated reports and documentation, ensuring that text remains both human-readable in its raw form and visually engaging once rendered with styling.

Within the R programming language and several other web development frameworks, there exists an md() function. This function typically interprets input text formatted in Markdown and converts it into HTML. For example, within the R package gt, which specializes in creating versatile tables and reports, the md() function allows the user to include Markdown-formatted strings in table cells, thereby enabling enhanced text formatting such as bold, italics, and hyperlinks.

Markdown File Extension (.md)

The file extension ".md" is widely recognized as indicative of files written in Markdown. These files are particularly popular on platforms such as GitHub and GitLab for README files and documentation purposes. The simple syntax of Markdown makes it accessible to users who require quick and efficient formatting without the complexities of full-fledged HTML or LaTeX. Applications like Microsoft Word (with certain plugins) and online editors like Dillinger can transform Markdown files into well-formatted HTML documents.

2. MD in Cryptography and Data Integrity

Message Digest Algorithms

Another interpretation of "MD" lies within the realm of cryptography. Here, MD often refers to message digest algorithms, such as MD5. The MD5 hashing function produces a 128-bit hash value, serving as a digital fingerprint for presented data. Although full security cannot be guaranteed due to vulnerabilities detected in MD5, it still finds utility in validation of data integrity, ensuring that data transfers or stored files have not been corrupted.

Usage of MD5 involves processing the data through the algorithm to produce a fixed-length string. This hash string acts as a checksum; any alteration to the source data typically results in a completely different hash, enabling quick verifications for integrity.

Furthermore, while the MD5 algorithm is a specific implementation of the broader concept of message digest functions, newer algorithms like SHA-256 are often recommended for higher security requirements. Nevertheless, the historical and ongoing relevance of MD-based hashing remains significant in legacy systems and non-critical applications where speed and simplicity are valued.

Merkle–Damgård Construction

Closely related to the idea of message digest algorithms is the Merkle–Damgård construction. Although not directly referred to as an "MD function," this construction technique is used to build cryptographic hash functions from secure compression functions. This methodology ensures that if the underlying compression function is collision-resistant, the overall hash function inherits that robustness. Understanding this construction is essential for grasping how many message digest algorithms are structurally implemented.

3. MD in Mathematical and Statistical Analysis

Minimum Distance Functions in ICA

An advanced application of the MD function exists within the field of Independent Component Analysis (ICA). When performing ICA, researchers and analysts aim to separate a set of signals into statistically independent components. To evaluate the performance of an algorithm that accomplishes this separation, a metric known as the Minimum Distance (MD) index is sometimes employed.

The MD index measures the difference between an estimated unmixing matrix \( \hat{W} \) and the true mixing matrix \( A \). For instance, the formula may be given by:

\( \[ MD(\hat{W}, A) = \frac{1}{\sqrt{p-1}} \inf_{P,D} ||PD \hat{W} A - I|| \] \)

In this expression, \( P \) represents a permutation matrix and \( D \) is a diagonal matrix with nonzero entries, and \( I \) is the identity matrix. This metric provides insight into how accurately the algorithm is able to disentangle mixed signals, making it an important analytical tool in signal processing and data analysis. While this interpretation of MD is more niche, it illustrates the adaptability of the concept across different academic disciplines.

4. MD in Command-Line Operations and Software Compilation

Directory Creation Command

Outside the realms of academic and research environments, the abbreviation "md" also appears as a command in various operating systems. In Windows, for instance, the command md (or mkdir in many other systems) is used to create directories and subdirectories from the command prompt. This operation is fundamental for organizing files and structuring the file system, and its simple usage underscores the practical utility of the MD function in everyday computing tasks.

Compiler Options in C/C++

In the context of software development, and particularly within the compiled languages C and C++, the "/MD" flag is frequently encountered. This compiler option instructs the compiler to link against a version of the runtime library that is optimized for multithreading and is suitable when building Dynamic Link Libraries (DLLs). This option is critical for ensuring that applications interact correctly with the runtime library on Windows operating systems, ensuring a balance between performance and compatibility in multithreaded environments.

Comparative Table of MD Function Uses

Context	Description	Practical Application
Programming Documentation	Processing and rendering Markdown text to HTML	Creating formatted documentation, README files, and reports
Cryptography	Utilization of MD5 and other message digest functions	Verifying data integrity and generating digital fingerprints
Mathematical/Statistical Analysis	Minimum Distance Functions in ICA evaluating separation quality	Assessing the accuracy of signal processing algorithms
Command-Line Operations	`md` or `mkdir` for directory creation	File system organization and structure creation in operating systems
Compiler Options	`/MD` flag for linking multithreaded runtime libraries	Software development in C/C++ on Windows platforms

Detailed Analysis by Context

Programming and Documentation

Markdown plays a pivotal role in modern programming and documentation efforts. The md() function in R, for example, is designed to interpret text that has been crafted in Markdown and transform it into HTML. This has marked benefits in generating dynamic content where static formatting may otherwise limit usability. Developers can embed lightweight formatting cues directly into code comments or documentation, making the resultant output more cohesive and visually appealing.

Real-World Usage

On many platforms such as GitHub, Markdown is the go-to format for documentation. This is attributable to its readability and straightforward syntax. Tools such as Dillinger allow users to convert Markdown text to HTML on the fly, which can then be embedded into web pages or software documentation sites. As Markdown has a relatively gentle learning curve, it is immensely popular among software developers, technical writers, and content managers.

Cryptographic Functions and Data Integrity

Moving to the cryptographic side, MD functions, notably MD5, have historically been used for quickly verifying file integrity. Although MD5 is less favored in high-security applications due to identified vulnerabilities, it remains in use where non-critical integrity checks are necessary. The function works by condensing variable-length data into a fixed-length hash, making it possible to determine whether data has been altered or corrupted during transmission.

Relevance in Modern Systems

Despite the push towards more robust algorithms like SHA-256, the legacy of MD-based algorithms endures, particularly in systems where performance and speed outweigh the need for heavy security measures. Its straightforward implementation also makes it a preferred choice in embedded systems and resource-constrained environments.

Mathematics and Signal Processing

The utilization of the MD function as a Minimum Distance metric in Independent Component Analysis (ICA) demonstrates the breadth of its application. In fields such as signal processing, separating mixed signals into individual, independent components is essential. The MD index provides a quantitative measure of how well the separation is achieved by comparing the estimated unmixing matrix with the true mixing configuration. This analysis is crucial for applications ranging from biomedical signal processing to financial time-series analysis.

Mathematical Representation

As noted earlier, the MD index is defined by a formula that involves matrices and norm calculations. This mathematical representation offers insight into the algorithm's performance and helps researchers optimize the separation process. With tools like R and MATLAB at their disposal, analysts can simulate various conditions and fine-tune their approaches using the Minimum Distance metric.

Command-Line Operations and Software Compilation

In everyday computing, the command md is frequently encountered. This command is essential for creating directories in command-line interpreters, such as Command Prompt on Windows. Its utility lies in its simplicity and universality across different scripts and automated processes where directory creation is required.

Compiler and Software Development Applications

For developers working with C/C++ on Windows, the /MD compiler flag is an important option. By linking the executable to a specialized version of the runtime library optimized for multithreading, developers ensure that their software is both efficient and capable of handling dynamic loads. This attention to runtime configuration is critical in today's high-performance computing environments, ensuring that applications behave predictably under varying operating conditions.