Ithy - Unlocking the Secrets of Spring Stretching: How Much Weight?

Key Insights

Consistent Behavior: The spring follows Hooke’s Law, demonstrating a direct proportionality between force and displacement.
Spring Constant (k): With an initial condition of 25 N stretching the spring 10 mm (0.01 m), the spring constant is calculated as 2500 N/m.
Extended Limit Analysis: With the extended limit at 80 mm (0.08 m), applying Hooke’s Law yields a weight of 200 N.

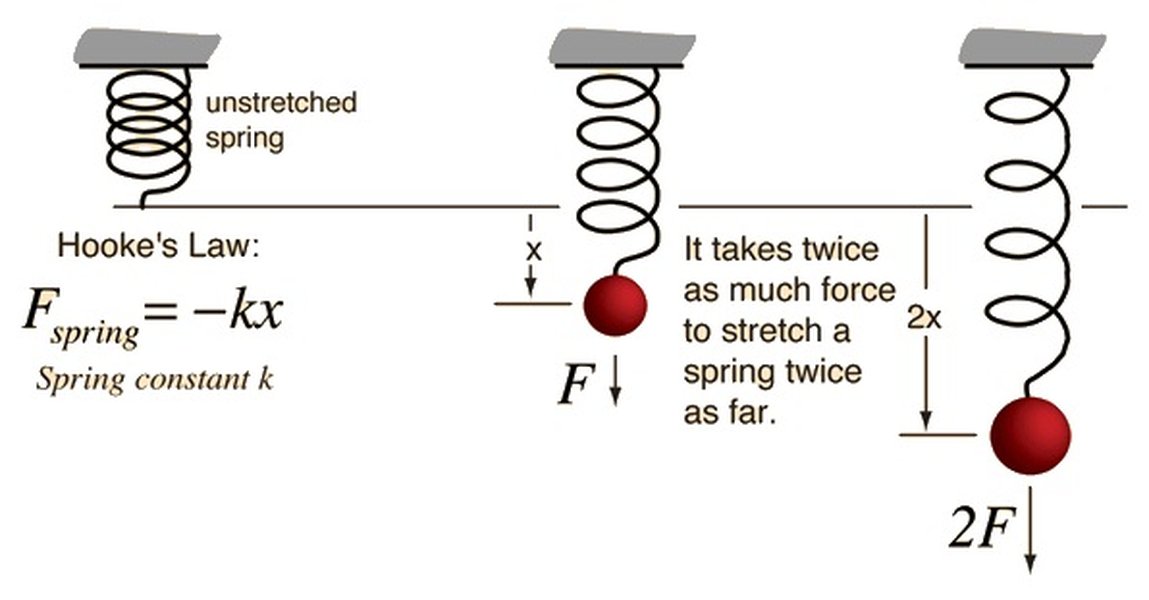
Understanding Hooke’s Law and the Spring Constant

Hooke’s Law is a foundational principle in physics that describes how springs behave when forces are applied. The law states that the force (F) required to stretch or compress a spring is directly proportional to the displacement (x) from its equilibrium position. This relationship is expressed mathematically as:

Mathematical Formulation

Using MathJax for clarity, we express Hooke’s Law as: \[ F = k \Delta x \] where:

\(F\) is the force in Newtons (N).
\(k\) is the spring constant, expressed in Newtons per meter (N/m).
\(\Delta x\) is the displacement in meters (m).

Given the condition that a force of 25 N causes a displacement of 10 mm (0.01 m), the slope or the spring constant (k) can be derived by rearranging the formula to:

\(\displaystyle k = \frac{F}{\Delta x} = \frac{25\, \text{N}}{0.01\, \text{m}} = 2500\, \text{N/m}\)

This constant remains valid as long as the spring remains within the elastic region, meaning the deformation is reversible.

Calculating the Force for an Extended Limit

With the spring’s behavior confirmed under the initial condition, we now analyze what happens when the spring is allowed a greater stretch. In the original scenario, the spring’s limit was reached at 50 mm. However, if the same spring reaches its limit at 80 mm, the analysis proceeds as follows:

Step-by-Step Calculation

1. Convert Millimeters to Meters

Since SI units require meters, convert the displacement:
\(80\, \text{mm} = 0.08\, \text{m}\)

2. Apply Hooke’s Law

The force in this new scenario is calculated using:
\(\displaystyle F = k \Delta x\)

Substituting known values:
\(\displaystyle F = 2500\, \text{N/m} \times 0.08\, \text{m} = 200\, \text{N}\)

Therefore, stretching the spring to an 80 mm limit requires a force of 200 N.

Visualizing the Relationship: A Radar Chart Representation

The following radar chart provides an intuitive visualization of the spring’s performance parameters. The chart displays datasets such as the force applied at different displacements, the spring constant consistency, and the extension limits. This visualization reinforces how linear the relationship is within the spring's elastic region.

Conceptual Map: Understanding the Spring Stretching Problem

The following diagram presents a simplified mind map illustrating the key steps from initial force application through to the extended limit calculation. This diagram helps to visually organize the chain of reasoning behind the final answer.

mindmap root["Spring Stretch Problem"] Origins["Initial Condition"] Force["25 N"] Displacement["10 mm"] k["2500 N/m"] Hooke["Hooke's Law"] Equation["F = kx"] Verification["Verified for various displacements"] Extended["Extended Limit Scenario"] NewLimit["80 mm (0.08 m)"] Calculation["F = 2500 * 0.08 = 200 N"] Result["Final Weight"] Weight["200 N Required"]

Summary Table: Calculation Steps and Results

The table below offers a concise summary of each step in the analysis along with the corresponding values:

Step	Description	Calculation/Value
Initial Force	Force to stretch by 10 mm	25 N
Displacement Conversion	10 mm in m	0.01 m
Spring Constant	\( k = \frac{F}{x} \)	2500 N/m
New Displacement	80 mm in m	0.08 m
Final Force Calculation	\( F = k \times x \)	200 N

Interactive Learning Material

For a deeper understanding of Hooke’s Law and the calculation of spring constants, consider exploring this educational video which walks through the underlying concepts with practical demonstrations: