
How Does AdaBoost Actually Learn from Mistakes? Unpacking the Adaptive Boosting Engine
Discover the iterative magic behind AdaBoost, transforming simple models into a powerful predictive force by focusing on errors.
Key Insights into AdaBoost
- Adaptive Learning: AdaBoost focuses on training examples that previous models misclassified by increasing their weights, forcing subsequent models to pay more attention to difficult cases.
- Sequential Ensemble: It builds a strong classifier by sequentially combining multiple simple models (weak learners), typically decision stumps, where each new model corrects the errors of its predecessors.
- Weighted Combination: The final prediction is made via a weighted majority vote of all weak learners, where more accurate models have a greater influence on the outcome.
Understanding AdaBoost: The Adaptive Ensemble Technique
AdaBoost, short for Adaptive Boosting, is a highly effective ensemble learning algorithm primarily used for classification tasks, though adaptable for regression. Developed by Yoav Freund and Robert Schapire, its strength lies in its ability to combine multiple "weak" classifiers—models that perform only slightly better than random chance—into a single, robust "strong" classifier. The core idea is iterative refinement: the algorithm learns sequentially, focusing more intensely on the data points that previous models found difficult to classify correctly.
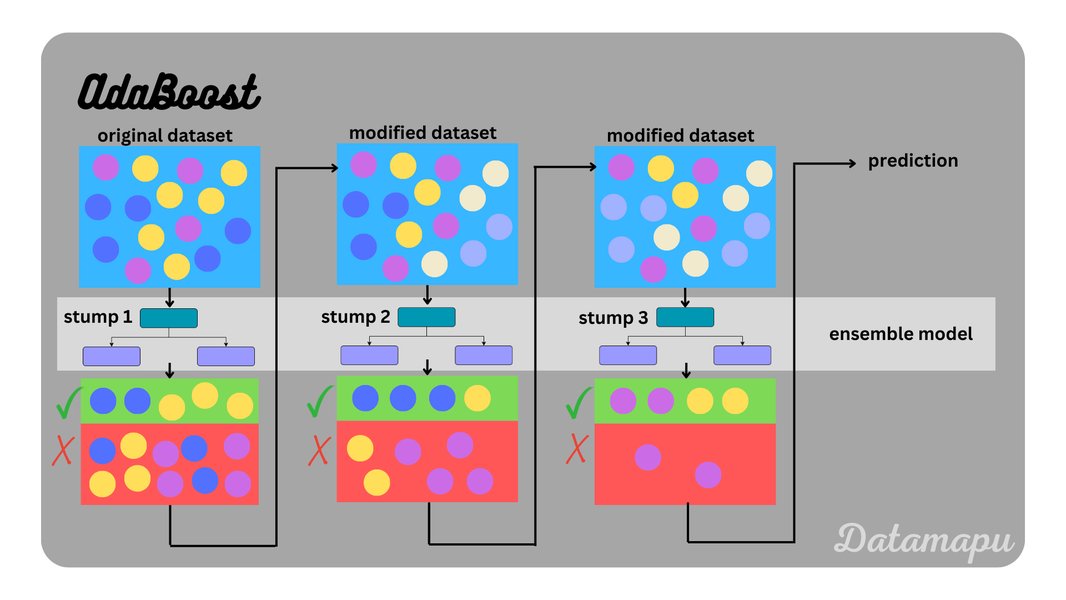
Conceptual overview of AdaBoost's iterative process.
The Step-by-Step Mechanics of AdaBoost
AdaBoost follows a structured, iterative process to build its powerful ensemble model. Let's break down how it works:
Step 1: Initialize Sample Weights
The algorithm begins by assigning an equal weight to every training sample. If there are \(N\) samples in the dataset, each sample \(i\) starts with a weight \(w_i = \frac{1}{N}\). This ensures that initially, all data points have the same level of importance for training the first weak learner.
Step 2: Train a Weak Learner
In the first iteration (and subsequent ones), a weak learner is trained on the training dataset, considering the current weights of the samples. A common choice for a weak learner is a decision stump – a decision tree with only one split (one node and two leaves). The goal of this weak learner \(h_t(x)\) at iteration \(t\) is to minimize the weighted classification error on the training data.
Step 3: Calculate the Weighted Error
Once the weak learner \(h_t\) is trained, its performance is evaluated by calculating its weighted error rate, \(\epsilon_t\). This error is the sum of the weights of the training samples that the weak learner misclassified:
\[ \epsilon_t = \sum_{i=1}^{N} w_i^{(t)} \cdot I(y_i \neq h_t(x_i)) \]Here, \(w_i^{(t)}\) is the weight of sample \(i\) at iteration \(t\), \(y_i\) is the true label of sample \(x_i\), \(h_t(x_i)\) is the prediction of the weak learner for sample \(x_i\), and \(I(\cdot)\) is the indicator function (1 if the condition inside is true, 0 otherwise). The error \(\epsilon_t\) must be less than 0.5 for the learner to be considered "weak" (better than random guessing).
Step 4: Compute the Learner's Weight (Alpha)
Each weak learner is assigned a weight, \(\alpha_t\), which reflects its performance. More accurate learners (lower error \(\epsilon_t\)) are given higher weights, signifying greater influence in the final ensemble prediction. The weight \(\alpha_t\) is calculated as:
\[ \alpha_t = \frac{1}{2} \ln \left( \frac{1 - \epsilon_t}{\epsilon_t} \right) \]Notice that as \(\epsilon_t\) approaches 0 (perfect classification), \(\alpha_t\) goes to infinity. Conversely, if \(\epsilon_t\) is 0.5 (random guessing), \(\alpha_t\) is 0. If \(\epsilon_t > 0.5\), \(\alpha_t\) becomes negative, which typically indicates an issue or the need to stop.
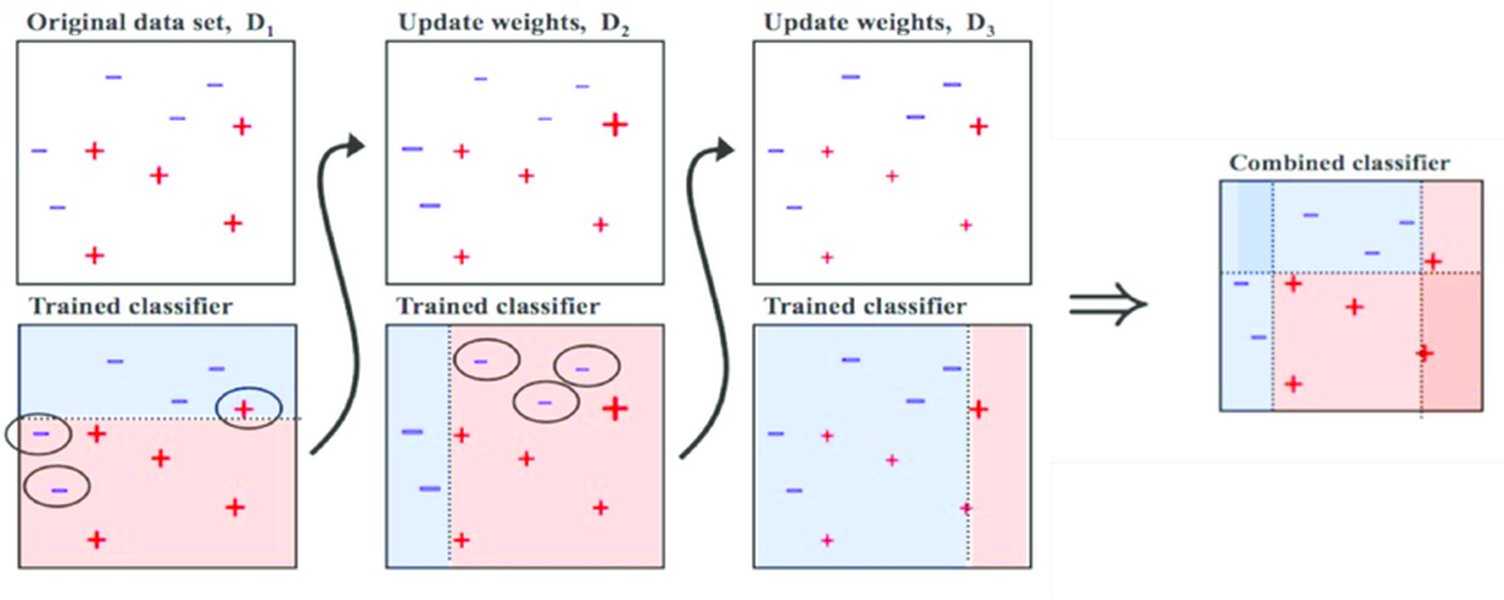
Visualizing the adaptive weight adjustment for misclassified samples.
Step 5: Update Sample Weights
This is the "adaptive" core of AdaBoost. The weights of the training samples are updated for the next iteration (\(t+1\)). The weights of misclassified samples are increased, while the weights of correctly classified samples are decreased. This ensures that the next weak learner focuses more on the samples that the current learner struggled with. The update rule is:
\[ w_i^{(t+1)} = w_i^{(t)} \cdot \exp(\alpha_t \cdot I(y_i \neq h_t(x_i))) \]Alternatively, this can be written as:
- For misclassified samples (\(y_i \neq h_t(x_i)\)): \(w_i^{(t+1)} = w_i^{(t)} \cdot e^{\alpha_t}\) (Weight increases)
- For correctly classified samples (\(y_i = h_t(x_i)\)): \(w_i^{(t+1)} = w_i^{(t)} \cdot e^{-\alpha_t}\) (Weight decreases)
After updating, the weights are typically normalized so that they sum to 1 (\(\sum_{i=1}^{N} w_i^{(t+1)} = 1\)). This normalization turns the weights into a probability distribution for potential sampling in some variants or simply keeps the weights scaled for the next learner's training.
Step 6: Repeat for Multiple Iterations
Steps 2 through 5 are repeated for a predefined number of iterations, \(T\) (a hyperparameter), or until a certain performance threshold is met. Each iteration produces a new weak learner \(h_t\) and its corresponding weight \(\alpha_t\).
Step 7: Combine Weak Learners for Final Prediction
The final strong classifier \(H(x)\) is formed by combining the predictions of all \(T\) weak learners. The combination is done through a weighted majority vote, using the calculated learner weights \(\alpha_t\). For a new input \(x\), the final prediction is typically determined by the sign of the weighted sum:
\[ H(x) = \text{sign} \left( \sum_{t=1}^{T} \alpha_t h_t(x) \right) \]In a binary classification setting (e.g., classes +1 and -1), if the sum is positive, the prediction is +1; if negative, the prediction is -1. The magnitude of the sum can also indicate the confidence of the prediction.
Visualizing AdaBoost's Core Concepts
The following mindmap illustrates the key components and relationships within the AdaBoost algorithm, helping to visualize its structure and adaptive nature.
Deeper Dive: AdaBoost Explained Visually
For a more intuitive understanding of how AdaBoost iteratively focuses on errors and combines weak learners, the following video provides a clear, step-by-step visual explanation of the algorithm's mechanics.
This video walks through a simple example, demonstrating how data point weights are adjusted after each decision stump is trained, and how these stumps are combined with varying importance (\(\alpha\) weights) to form the final, more accurate model.
Key Characteristics and Considerations
AdaBoost possesses several distinct features:
- Sequential Nature: Unlike parallel ensemble methods like Bagging (used in Random Forests), AdaBoost builds its learners sequentially. Each new learner's training depends heavily on the performance and errors of the preceding ones.
- Focus on Errors: Its primary strength lies in its ability to hone in on difficult-to-classify examples, effectively reducing the model's bias.
- Flexibility with Weak Learners: While decision stumps are common, AdaBoost can technically use any classification algorithm as a weak learner, as long as it performs better than random chance.
- Sensitivity to Noise and Outliers: Because AdaBoost increases the weights of misclassified points, noisy data or outliers that are inherently hard to classify can receive extremely high weights. This can sometimes lead the algorithm to overfit to these noisy points if not carefully managed (e.g., by limiting the number of iterations or using regularization).
- Exponential Loss Function: Mathematically, AdaBoost can be shown to minimize an exponential loss function, which heavily penalizes misclassifications.
AdaBoost vs. Bagging (Random Forest)
Understanding AdaBoost often involves comparing it to other ensemble techniques like Bagging, which forms the basis of Random Forests. The table below highlights key differences:
| Feature | AdaBoost (Boosting) | Bagging (e.g., Random Forest) |
|---|---|---|
| Model Building | Sequential (learners depend on previous ones) | Parallel (learners are independent) |
| Sample Weighting | Adaptive weights (misclassified samples get higher weights) | Equal weights (via bootstrapping/random sampling) |
| Learner Type | Typically weak learners (e.g., decision stumps) | Typically strong learners (e.g., deep decision trees) |
| Focus | Reducing Bias | Reducing Variance |
| Voting | Weighted majority vote (based on learner accuracy) | Simple majority vote (or averaging for regression) |
| Sensitivity to Noise | Higher sensitivity | Lower sensitivity |
Performance Profile: AdaBoost in Context
To understand where AdaBoost excels and where it might face challenges compared to other popular ensemble methods like Random Forest and Gradient Boosting (another boosting technique), consider the following comparative assessment across several dimensions. Note that performance can vary significantly based on the specific dataset and hyperparameter tuning.
This chart provides a relative comparison based on typical algorithm behaviors. AdaBoost generally excels at reducing bias and can achieve high accuracy, but its sequential nature can make training slower than parallel methods like Random Forest, and its sensitivity to noise requires careful handling.
Frequently Asked Questions (FAQ)
What exactly is a "weak learner" in AdaBoost?
A weak learner, or base estimator, is a classifier that performs only slightly better than random chance on a given classification task. For a binary classification problem, this means having an accuracy just above 50%. Decision stumps (simple decision trees with only one split) are the most common weak learners used with AdaBoost because they are computationally inexpensive and meet the "weak" criterion. The power of AdaBoost comes from combining many such simple, weak models into a strong, highly accurate ensemble.
Why is AdaBoost considered "adaptive"?
AdaBoost is adaptive because it adjusts its approach in each iteration based on the errors made by the previous models. Specifically, it increases the weights of training samples that were misclassified in the previous iteration. This forces the next weak learner in the sequence to focus more attention on these "harder" examples. This iterative adaptation to the data's difficulty is the defining characteristic of AdaBoost.
Is AdaBoost sensitive to noisy data and outliers?
Yes, AdaBoost can be quite sensitive to noisy data and outliers. Because the algorithm adaptively increases the weights of misclassified samples, outliers or noisy samples that are inherently difficult or impossible to classify correctly can end up with very large weights. This can cause subsequent weak learners to focus excessively on these erroneous points, potentially leading to overfitting and degrading the overall performance of the model on unseen data. Techniques like outlier removal or using modified versions of AdaBoost can sometimes mitigate this issue.
Can AdaBoost be used for regression problems?
Yes, while AdaBoost was originally designed for classification, variants like AdaBoost.R and AdaBoost.RT have been developed for regression tasks. The core idea remains similar: iteratively fitting weak learners (regressors in this case) to the data, focusing on samples where the previous models had larger errors. The way errors are measured and weights are updated differs from the classification version to suit the continuous nature of regression targets.
Recommended Reading
- Explore the differences and similarities between AdaBoost and Gradient Boosting Machine (GBM).
- Learn about the key hyperparameters in AdaBoost and strategies for optimizing them.
- Discover practical examples of how AdaBoost is used in various fields like image recognition and finance.
- Delve into the mathematical foundations of AdaBoost, including its connection to exponential loss minimization.
References
Last updated May 4, 2025