
Unraveling Recursion: A Deep Dive into Self-Referential Processes
Explore the fundamental concept of recursion, its mechanisms, diverse applications, and critical considerations across various disciplines.
Key Insights into Recursion
- Self-Definition at Its Core: Recursion is fundamentally about defining a problem, concept, or process in terms of itself or a simpler version of itself, allowing for the decomposition of complex challenges into manageable parts.
- Dual Nature: Base and Recursive Cases: Every recursive solution hinges on two crucial components: a "base case" that provides a direct, non-recursive solution and acts as the stopping condition, and a "recursive case" where the function calls itself with a modified, typically smaller, input.
- Ubiquitous Applications: From mathematical computations like factorials and Fibonacci sequences to advanced data structure traversals (trees and graphs), sorting algorithms (Quicksort, Mergesort), and even linguistic structures, recursion is a powerful and elegant tool for solving problems with inherent self-similar structures.
Recursion, derived from the Latin "recurrere" meaning "to run back or return," is a profound concept prevalent in mathematics, computer science, linguistics, and logic. It encapsulates the idea of a process or definition referring to itself, enabling the solution of intricate problems by breaking them down into simpler, self-similar instances.
The Essence of Recursion: Defining Self-Reference
At its heart, recursion involves a concept or process that is defined in terms of itself or a simpler version of itself. This self-referential nature allows for a powerful problem-solving paradigm, especially in areas where problems naturally exhibit nested or hierarchical structures.
Fundamental Components of Recursive Solutions
For any recursive process to be well-defined and terminate correctly, two essential components must be present:
The Base Case: The Crucial Stopping Point
The base case is the simplest instance of the problem that can be solved directly without any further recursive calls. It serves as the termination condition for the recursion, preventing infinite loops and ensuring that the process eventually yields a result. Without a properly defined base case, a recursive function would call itself indefinitely, leading to an "infinite recursion" and ultimately a "stack overflow" error, as the program's call stack exhausts its allocated memory.
The Recursive Case: The Path to Simplification
The recursive case is the part of the function where it calls itself with a modified input. This input is typically a smaller or simpler instance of the original problem, bringing the problem progressively closer to the base case. The function performs some minimal work and then delegates the rest of the problem to a recursive call, embodying the "divide-and-conquer" approach.
How Recursion Functions Internally: The Call Stack Mechanism
In programming, when a recursive function is invoked, its execution flow is managed by the program's call stack. This mechanism is crucial to understanding how recursion works:
When a function is called, a "stack frame" is created and pushed onto the program's call stack. This stack frame contains all the necessary information for that specific function invocation, including its local variables, parameters, and the return address (where the program should resume execution after the function completes). In the context of recursion, each time the function calls itself, a new stack frame is pushed onto the call stack. This creates multiple active instances of the same function, each with its own set of variables and execution context. The call stack operates on a Last-In, First-Out (LIFO) principle, meaning the last function called is the first one to complete and return.
Visualizing the recursive call stack with a factorial example.
When the base case is eventually reached, the function returns a value, and its corresponding stack frame is popped off the call stack. Control then passes back to the function that made the call (the previous stack frame), resuming execution from the point of the recursive call. This unwinding process continues until the initial function call at the bottom of the stack is resolved, providing the final solution.
Illustrative Examples of Recursion in Action
Recursion is best understood through concrete examples that demonstrate its elegance and power in problem-solving:
Factorial Calculation
The factorial of a non-negative integer \(n\), denoted as \(n!\), is the product of all positive integers less than or equal to \(n\). This is a quintessential example of a problem naturally suited for recursion:
\[ \text{factorial}(n) = \begin{cases} 1 & \text{if } n = 0 \text{ or } n = 1 \ n \times \text{factorial}(n-1) & \text{if } n > 1 \end{cases} \]
function factorial(n):
if n == 0 or n == 1: // Base case
return 1;
else: // Recursive case
return n * factorial(n - 1);
For example, to calculate factorial(5):
- factorial(5) calls factorial(4)
- factorial(4) calls factorial(3)
- factorial(3) calls factorial(2)
- factorial(2) calls factorial(1)
- factorial(1) is the base case, returns 1.
Then, the results are multiplied back up the stack: 2 * 1 = 2, 3 * 2 = 6, 4 * 6 = 24, 5 * 24 = 120.
Fibonacci Sequence
The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, typically starting with 0 and 1 (e.g., 0, 1, 1, 2, 3, 5, 8, ...). Its definition is inherently recursive:
\[ \text{fibonacci}(n) = \begin{cases} n & \text{if } n \le 1 \ \text{fibonacci}(n-1) + \text{fibonacci}(n-2) & \text{if } n > 1 \end{cases} \]
function fibonacci(n):
if n <= 1: // Base case
return n;
else: // Recursive case
return fibonacci(n - 1) + fibonacci(n - 2);
Tree and Graph Traversal
Recursion is exceptionally well-suited for navigating and processing hierarchical data structures like trees (e.g., binary trees, file systems) and graphs. Algorithms such as Depth-First Search (DFS) naturally employ recursion to explore nodes and their descendants.
function traverse(node):
if node is null: // Base case
return;
process(node); // Perform an operation on the current node
traverse(node.left); // Recursively visit left child
traverse(node.right); // Recursively visit right child
Diverse Applications of Recursion
Recursion finds extensive use across various domains, particularly in computer science and algorithmic design:
An analytical radar chart showcasing the diverse applications and characteristics of recursion across different domains.
Sorting and Searching Algorithms
Many efficient sorting algorithms, such as Quicksort and Mergesort, are built upon the divide-and-conquer paradigm, which naturally lends itself to recursive implementation. Binary search, a highly efficient search algorithm for sorted arrays, also utilizes recursion to repeatedly halve the search space.
Data Structure Manipulation
Beyond simple traversal, recursion is fundamental for operations on complex data structures like trees (e.g., insertion, deletion, balancing in binary search trees) and graphs (e.g., finding paths, connected components). Its ability to process nested structures elegantly makes it indispensable.
Mathematical Computations
As seen with factorials and Fibonacci sequences, many mathematical functions and sequences have recursive definitions, making recursion a natural fit for their computation. This also extends to problems involving permutations, combinations, and powers.
Algorithmic Puzzles and Backtracking
Classic algorithmic puzzles like the Tower of Hanoi, or problem-solving techniques such as backtracking (used in Sudoku solvers or maze generation/solving), rely heavily on recursion to explore different possibilities and revert when a dead end is reached.
Parsing and Compilers
Compilers and interpreters often use recursive descent parsers to analyze the grammatical structure of programming languages. The hierarchical nature of language syntax (e.g., expressions nested within statements) perfectly aligns with recursive definitions.
Fractal Generation and Graphics
Creating fractals, which are intricate, self-similar geometric patterns, is often achieved through recursive algorithms. Each part of a fractal can be seen as a smaller version of the whole, a characteristic perfectly captured by recursion.
Advantages and Disadvantages of Recursion
While recursion is a powerful tool, it comes with its own set of benefits and potential pitfalls:
| Aspect | Advantages of Recursion | Disadvantages of Recursion |
|---|---|---|
| Code Simplicity & Readability | Often leads to more concise, elegant, and readable code for problems with inherent recursive structures (e.g., tree traversals). | Can be harder to trace and debug due to multiple function calls on the call stack, especially for beginners. |
| Problem Decomposition | Excels at breaking down complex problems into smaller, manageable subproblems of the same type, aligning with "divide-and-conquer" strategies. | Can be less intuitive for problems that are more easily solved iteratively (with loops). |
| Memory Usage | Leverages the call stack for managing intermediate states without explicit data structures. | Consumes more memory due to the overhead of creating a new stack frame for each recursive call. |
| Performance | For certain problems, it can be conceptually faster or more efficient in terms of development time. | May be slower than iterative solutions due to function call overhead and stack management. Risk of "stack overflow" error for excessively deep recursion. |
| Suitability | Ideal for problems that mirror mathematical recursive definitions or hierarchical data structures. | Not always the most efficient or practical solution; iterative approaches are often preferred for simple repetitive tasks. |
Beyond Programming: Recursion in Broader Contexts
The concept of recursion extends far beyond the realm of computer programming:
Traversal (Trees, Graphs)"] id4["Algorithms (Sort, Search)"] id5["Problem Solving (Divide & Conquer)"] id6["Stack Mechanics (Call Stack)"] id7["Mathematics"] id8["Recursive Definitions
(Factorial, Fibonacci)"] id9["Induction"] id10["Fractals"] id11["Linguistics"] id12["Nested Sentences
(Grammar Rules)"] id13["Self-Referential Structures"] id14["Logic & Philosophy"] id15["Paradoxes (Liar Paradox)"] id16["Self-Reference in Logic"] id17["Art & Design"] id18["Patterns that repeat
at different scales"] id19["Core Principles"] id20["Base Case
(Stopping Condition)"] id21["Recursive Case
(Simplification Step)"]
A mindmap illustrating the various domains and core principles where recursion plays a significant role.
Mathematics
In mathematics, recursion is fundamental to defining sequences, sets, and functions. Recursive definitions, like those for factorials or the Fibonacci sequence, specify how to construct elements based on preceding ones. Mathematical induction, a proof technique, also inherently uses a recursive pattern.
Linguistics and Grammar
Human language exhibits recursive structures, allowing for the embedding of phrases within phrases or sentences within sentences. For example, "This is the house that Jack built" can be extended recursively: "This is the cat that chased the rat that lived in the house that Jack built." This recursive capacity allows for infinite linguistic complexity.
Fractals and Art
Fractals are geometric shapes that exhibit self-similarity at different scales; zooming into any part of a fractal reveals patterns identical or very similar to the whole. This characteristic is a direct manifestation of recursive principles in visual form, often generated by recursive algorithms.
Understanding Recursion Visually
Visual explanations can significantly enhance comprehension of recursion, particularly how function calls are managed and resolved. This video provides an excellent visual breakdown:
This video provides an animated explanation of how recursion works internally, showing the dynamic interaction with the call stack, which is critical for grasping the concept beyond theoretical definitions.
Frequently Asked Questions About Recursion
Conclusion: Recursion's Enduring Importance
Recursion stands as a foundational and elegant concept in computing and beyond. Its ability to simplify complex problems by defining them in terms of themselves makes it an indispensable tool for tackling challenges that possess inherent self-similar or hierarchical structures. While requiring careful implementation to manage memory and prevent errors like stack overflows, its power in problem decomposition, code conciseness, and alignment with mathematical definitions ensures its enduring relevance in algorithm design, data structure manipulation, and even the fundamental understanding of language and natural patterns. Mastering recursion not only equips one with a potent problem-solving technique but also deepens one's understanding of computational thinking.
Recommended Further Exploration
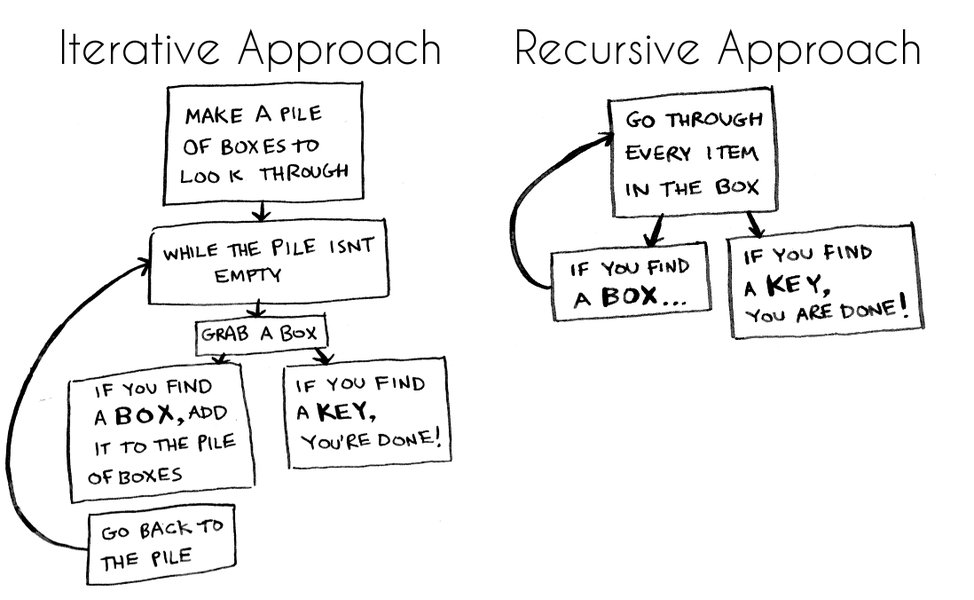
- How to avoid stack overflows in recursive functions?
- What are the key differences between recursion and iteration, and when to use each?
- How do compilers optimize tail recursion, and what are its benefits?
- Where is recursion applied in advanced AI algorithms and data processing?