Understanding the Vector Space Model (VSM) in Information Retrieval and NLP

The Vector Space Model (VSM) is a foundational concept in information retrieval and natural language processing (NLP) that provides a powerful way to represent and analyze textual data. At its core, the VSM transforms documents and queries into numerical vectors within a multi-dimensional space. This transformation allows for the quantification of relationships, such as similarity and relevance, between pieces of text using mathematical and geometric principles.

Key Highlights of the Vector Space Model

Vector Representation: The VSM represents documents and queries as vectors in a multi-dimensional space, where each dimension typically corresponds to a unique term in the vocabulary.
Measuring Similarity: The similarity between documents or between a document and a query is measured by the distance or angle between their corresponding vectors, most commonly using cosine similarity.
Applications: VSM is widely used in information retrieval systems, search engines, text classification, document clustering, and other text-based machine learning tasks.

The Core Concept: Representing Text as Vectors

The fundamental idea behind the Vector Space Model is to move away from treating text as a sequence of words and instead represent it as numerical vectors. This allows us to apply mathematical operations to analyze and compare text data. Imagine each unique term in a collection of documents as a dimension in a multi-dimensional space. A document is then represented as a point in this space, with the coordinates of the point determined by the importance or frequency of each term within the document.

This transformation is crucial because computers can easily process numerical data and perform calculations like measuring distances or angles between vectors. This numerical representation opens up possibilities for various computational tasks on text, such as finding documents similar to a given query or grouping similar documents together.

Building the Vector Space: The Document-Term Matrix

A key step in implementing the VSM is creating a document-term matrix. This matrix is a tabular representation where rows represent documents and columns represent the unique terms (vocabulary) across all documents. The values within the matrix represent the weight of each term in each document. This weight signifies the importance of a term within a specific document. A common and effective weighting scheme is Term Frequency-Inverse Document Frequency (TF-IDF).

Term Frequency (TF)

Term Frequency measures how often a term appears in a document. The more frequent a term is in a document, the higher its importance within that document. A simple way to calculate TF is to count the occurrences of a term in a document. However, raw counts can be misleading, so variations like logarithmic scaling or normalization are often used.

Inverse Document Frequency (IDF)

Inverse Document Frequency measures the rarity of a term across the entire collection of documents. Terms that appear in many documents are less discriminative than terms that appear in only a few. IDF assigns a higher weight to rarer terms, thus giving them more importance in determining the uniqueness of a document.

The IDF for a term is typically calculated as the logarithm of the total number of documents divided by the number of documents containing the term.

\[ \text{IDF}(t) = \log \left( \frac{\text{Total number of documents}}{\text{Number of documents containing term } t} \right) \]

TF-IDF Weighting

The TF-IDF weight for a term in a document is the product of its TF and IDF scores. This weighting scheme balances the local importance of a term within a document (TF) with its global importance across the document collection (IDF).

\[ \text{TF-IDF}(t, d) = \text{TF}(t, d) \times \text{IDF}(t) \]

The TF-IDF values populate the document-term matrix, where each entry (i, j) represents the TF-IDF weight of term j in document i. Once this matrix is constructed, each row (representing a document) becomes a vector in the multi-dimensional term space.

Measuring Similarity: The Cosine Similarity

With documents and queries represented as vectors, we can now quantify their similarity. The Vector Space Model uses geometric measures to determine how "close" two vectors are in the multi-dimensional space. The most widely used similarity measure in VSM is cosine similarity.

Cosine similarity measures the cosine of the angle between two vectors. A cosine similarity of 1 indicates that the vectors are perfectly aligned (meaning the documents are very similar), a cosine similarity of 0 indicates that the vectors are orthogonal (meaning there is no similarity, or the terms in one do not appear in the other), and a cosine similarity of -1 indicates that the vectors are completely opposite.

The formula for cosine similarity between two vectors, A and B, is:

\[ \text{Cosine Similarity}(A, B) = \frac{A \cdot B}{||A|| \cdot ||B||} \]

Where \(A \cdot B\) is the dot product of vectors A and B, and \(||A||\) and \(||B||\) are the magnitudes (or Euclidean norms) of vectors A and B, respectively.

\[ A \cdot B = \sum_{i=1}^{n} A_i B_i \] \[ ||A|| = \sqrt{\sum_{i=1}^{n} A_i^2} \] \[ ||B|| = \sqrt{\sum_{i=1}^{n} B_i^2} \]

In the context of VSM, vectors A and B can represent a document and a query, or two different documents. A higher cosine similarity score indicates greater similarity between the corresponding text elements.

Why Cosine Similarity?

Cosine similarity is preferred over distance metrics like Euclidean distance in VSM for text analysis because it is not affected by the magnitude of the vectors. In text representation, the magnitude of a vector can be influenced by the length of the document. Cosine similarity focuses on the angle between the vectors, which reflects the similarity in the distribution of terms, regardless of the document length.

Applications of the Vector Space Model

The Vector Space Model has been instrumental in the development of various applications in information retrieval and natural language processing.

Information Retrieval and Search Engines

The most prominent application of VSM is in information retrieval systems and search engines. When a user submits a query, the query is also converted into a vector using the same process as documents. The system then calculates the similarity (typically cosine similarity) between the query vector and the vector of each document in the collection. Documents are then ranked based on their similarity scores, presenting the most relevant documents to the user first.

Here's a simplified representation of the information retrieval process:

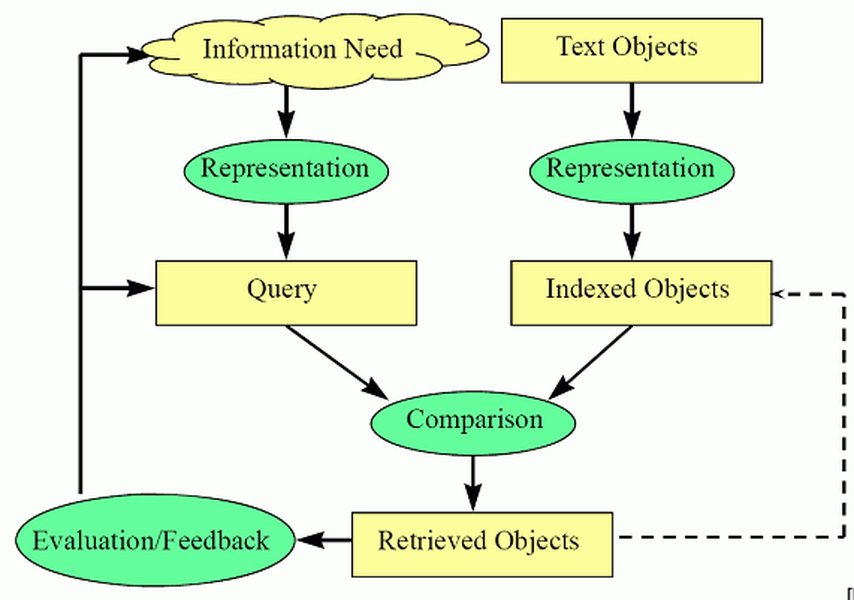
Figure: A general diagram illustrating the information retrieval process.

Text Classification

VSM is also used in text classification tasks. Documents are represented as vectors, and these vectors are used as features to train machine learning models (such as Naive Bayes, Support Vector Machines, or neural networks) to classify documents into predefined categories.

Document Clustering

Document clustering involves grouping similar documents together. By representing documents as vectors, clustering algorithms (like K-means) can be applied to group documents based on the proximity of their corresponding vectors in the vector space.

Text Similarity Analysis

Beyond information retrieval, VSM can be used to measure the similarity between any two pieces of text, such as sentences or paragraphs. This is useful in applications like plagiarism detection, document summarization, and question answering systems.

Advantages and Limitations of the Vector Space Model

While the VSM is a powerful and widely used model, it has both advantages and limitations.

Advantages

Simplicity and Interpretability: The VSM is conceptually simple and easy to understand. The vector representation and similarity measures have clear geometric interpretations.
Handling Partial Matches: Unlike earlier boolean models, VSM allows for partial matches between queries and documents, providing a ranking of results based on relevance.
Flexibility in Term Weighting: The framework allows for experimentation with different term weighting schemes (like TF-IDF and BM25) to improve retrieval performance.
Mathematical Foundation: The model is based on solid linear algebra, enabling the use of various mathematical tools and algorithms.

Limitations

High Dimensionality: The vector space can be very high-dimensional, especially with large vocabularies. This can lead to computational challenges and the "curse of dimensionality."
Sparsity: Document vectors are often very sparse, meaning most dimensions (terms) have a weight of zero. This is because most documents only contain a small subset of the entire vocabulary.
Lack of Semantic Understanding: The VSM treats terms as independent features, ignoring the semantic relationships between words (e.g., synonyms or related concepts). This can lead to poor retrieval results when a query uses different terms to describe the same concept as a relevant document.
Bag-of-Words Assumption: The classic VSM relies on the bag-of-words model, which disregards the order and context of words in a document. This can lead to a loss of important semantic information.

Despite its limitations, the Vector Space Model remains a fundamental concept and a strong baseline for many information retrieval and NLP tasks. Many advanced techniques and models build upon the principles of VSM, attempting to address its shortcomings, particularly regarding semantic understanding and dimensionality.

Addressing VSM Limitations and Future Directions

Researchers and practitioners have developed several approaches to mitigate the limitations of the classic Vector Space Model and enhance its capabilities.

Dimensionality Reduction

Techniques like Latent Semantic Analysis (LSA) and Singular Value Decomposition (SVD) are used to reduce the dimensionality of the vector space while preserving the most important information. This helps to address the high dimensionality and sparsity issues.

Incorporating Semantic Information

Models like Latent Dirichlet Allocation (LDA) and Word Embeddings (e.g., Word2Vec, GloVe, FastText) aim to capture the semantic relationships between words. These semantic representations can be integrated with VSM or used as alternative approaches to text representation.

Generalized Vector Space Model (GVSM)

The Generalized Vector Space Model attempts to address the independence assumption of terms in the classic VSM by considering the relationships between terms. This can involve incorporating co-occurrence information or using techniques from network analysis.

The field continues to evolve with the advent of deep learning models and transformer architectures, which offer sophisticated ways to represent and understand text. However, the fundamental principles of representing text as vectors and measuring similarity, as established by the Vector Space Model, continue to be relevant and inform modern approaches.

Illustrative Example

To illustrate the VSM, let's consider a simple example with two documents and a query.

Document 1: "The quick brown fox jumps over the lazy dog."

Document 2: "The lazy dog slept in the sun."

Query: "brown fox and lazy dog"

First, we identify the unique terms (vocabulary) in the documents and query: "the", "quick", "brown", "fox", "jumps", "over", "lazy", "dog", "slept", "in", "sun", "and".

Next, we create a document-term matrix using TF (for simplicity in this example, without IDF).

Term	Document 1 (TF)	Document 2 (TF)	Query (TF)
the	2	2	1
quick	1	0	0
brown	1	0	1
fox	1	0	1
jumps	1	0	0
over	1	0	0
lazy	1	1	1
dog	1	1	1
slept	0	1	0
in	0	1	0
sun	0	1	0
and	0	0	1

Now, we have vectors for each document and the query based on these term frequencies.

Vector D1 = [2, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0]

Vector D2 = [2, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0]

Vector Q = [1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 0, 1]

We can then calculate the cosine similarity between the query and each document to rank the documents based on relevance.

Watch a Video on the Vector Space Model

For a visual explanation of the basic idea behind the Vector Space Model, you can watch the following video:

Video: Lecture 5 — Vector Space Model Basic Idea from UIUC.

This video provides a concise overview of the fundamental principles of representing text as vectors in a multi-dimensional space, which is the core concept of the Vector Space Model. It helps to visualize how documents and queries are positioned in this space and how their relationships are determined geometrically.

Frequently Asked Questions about the Vector Space Model

What is the main purpose of the Vector Space Model?

The main purpose of the Vector Space Model is to represent text (like documents and queries) as numerical vectors in a multi-dimensional space. This allows for the computational analysis and comparison of text based on mathematical and geometric principles, primarily for tasks like information retrieval and text similarity.

How does VSM measure the similarity between documents?

VSM measures the similarity between documents by calculating the similarity (or distance) between their corresponding vectors in the multi-dimensional space. The most common measure is cosine similarity, which calculates the cosine of the angle between the vectors. A larger cosine value (closer to 1) indicates higher similarity.

What is TF-IDF and why is it used in VSM?

TF-IDF (Term Frequency-Inverse Document Frequency) is a common term weighting scheme used in VSM. It assigns a weight to each term in a document based on how frequently it appears in that document (TF) and how rare it is across the entire collection of documents (IDF). TF-IDF helps to capture the importance of terms within a document and their discriminative power across the corpus.

What are the main limitations of the classic VSM?

The main limitations of the classic VSM include high dimensionality, sparsity of vectors, lack of semantic understanding (it treats terms as independent), and the bag-of-words assumption which ignores word order and context.

How are the limitations of VSM being addressed?

Limitations of VSM are being addressed through techniques like dimensionality reduction (e.g., LSA, SVD), incorporating semantic information using word embeddings and other semantic models, and developing variations like the Generalized Vector Space Model.